x^2+2x^2y^2+2y^2-(x^2y^2+2x^2)-2=0 tim x va y
SN
Những câu hỏi liên quan
tim x va y biet rang
a) x2+2y2+2xy-2y +1=0
b) x2+2y2+2xy -2x+2=0
......................?
mik ko biết
mong bn thông cảm
nha ................
Đúng 0
Bình luận (0)
a) x2+2y2+2xy-2y+1=0
\(\Leftrightarrow\)(x2+2xy+y2)+(y2-2y+1)=0
\(\Leftrightarrow\)(x+y)2+(y-1)2=0
\(\Leftrightarrow\hept{\begin{cases}x+y=0\\y-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
Vậy x=-1, y=1
Đúng 0
Bình luận (0)
a/ \(x^2+2y^2+2xy-2y+1=0\)
<=> \(\left(x^2+2xy+y^2\right)+\left(y^2-2y+1\right)=0\)
<=> \(\left(x+y\right)^2+\left(y-1\right)^2=0\)
<=> \(\hept{\begin{cases}\left(x+y\right)^2=0\\\left(y-1\right)^2=0\end{cases}}\)
<=> \(\hept{\begin{cases}x+y=0\\y-1=0\end{cases}}\)
<=> \(\hept{\begin{cases}x=-y\\y=1\end{cases}}\)
<=> \(\hept{\begin{cases}x=-1\\y=1\end{cases}}\)
b/ \(x^2+2y^2+2xy-2x+2=0\)
<=> \(\left(x^2+2xy+y^2\right)+\left(2y-2x+2\right)=0\)
<=> \(\left(x+y\right)^2+2\left(y-x+1\right)=0\)
<=> \(\hept{\begin{cases}\left(x+y\right)^2=0\\2\left(y-x+1\right)=0\end{cases}}\)
<=> \(\hept{\begin{cases}x+y=0\\y-x+1=0\end{cases}}\)
<=> \(\hept{\begin{cases}x+y=0\\y-x=-1\end{cases}}\)
<=> \(\hept{\begin{cases}x+y=0\left(1\right)\\x-y=1\left(2\right)\end{cases}}\)
Trừ (1) và (2)
=> \(2y=-1\)
<=> \(y=-\frac{1}{2}\)
<=> \(x=\frac{1}{2}\)(vì \(x+y=0\)<=> \(x=-y\))
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tim 2 so tu nhien x va y biet 1) (2x+1)x(y-3)=10 2) (x+1)x(2y-5)=143 3) (3x-2)x(2y-3)=1 4) (x+1)x(2y-1)=12
bạn viết lại đi sai đề hay sao ý
Đúng 0
Bình luận (0)
Tim x,y,z biet: a,(3x−2y)6+(y−5z)8+|z−2|0(3x−2y)6+(y−5z)8+|z−2|0 b,3x−2y42x−4z3y−3z23x−2y42x−4z3y−3z2va x+y+z990Gấp gấp gấp!Tim x,y,z biet: a,(3x−2y)6+(y−5z)8+|z−2|0(3x−2y)6+(y−5z)8+|z−2|0 b,3x−2y42x−4z3y−3z23x−2y42x−4z3y−3z2va x+y+z990Gấp gấp gấp!
Đọc tiếp
Tim x,y,z biet: a,(3x−2y)6+(y−5z)8+|z−2|=0(3x−2y)6+(y−5z)8+|z−2|=0
b,3x−2y4=2x−4z3=y−3z23x−2y4=2x−4z3=y−3z2va x+y+z=990
Gấp gấp gấp!
Tim x,y,z biet: a,(3x−2y)6+(y−5z)8+|z−2|=0(3x−2y)6+(y−5z)8+|z−2|=0
b,3x−2y4=2x−4z3=y−3z23x−2y4=2x−4z3=y−3z2va x+y+z=990
Gấp gấp gấp!
vãi 4 năm mà ko mtj thằng nào rep đã thế còn gấp
tim x y z biết
a,4x^2+9y^2+4x-24y+17=0
b,2x^2+2y^2+z^2+2xy-2xz-6y+9=0
c,x^2+2y+2xy+2x+6y+5=0
tim x y z biết
a,4x^2+9y^2+4x-24y+17=0
b,2x^2+2y^2+z^2+2xy-2xz-6y+9=0
c,x^2+2y+2xy+2x+6y+5=0
\(a,4x^2+9y^2+4x-24y+17=0\)
\(\Rightarrow\left(4x^2+4x+1\right)+\left(9y^2-24y+16\right)=0\)
\(\Rightarrow\left(2x+1\right)^2+\left(3y-4\right)^2=0\)
\(\left(2x+1\right)^2\ge0;\left(3y-4\right)^2\ge0\)
\(\Rightarrow\hept{\begin{cases}\left(2x+1\right)^2=0\\\left(3y-4\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}2x+1=0\\3y-4=0\end{cases}\Rightarrow}\hept{\begin{cases}x=-\frac{1}{2}\\y=\frac{4}{3}\end{cases}}}\)
Đúng 1
Bình luận (1)
bn nào viết rõ hơn giùm mik đc ko.
(a^2+b^2)(x^2+y^2)=(ax+by)^2
<=> a^2x^2 + a^2y^2 + b^2x^2 + b^2y^2 = a^2x^2 + 2abxy + b^2y^2
<=> a^2y^2 + b^2x^2 = 2abxy
<=> a^2y^2 + b^2x^2 - 2abxy = 0
<=> (ay - bx)^2 = 0
=> ay - bx = 0
=> ay = bx
=> a/x = b/y ( x,y khác 0)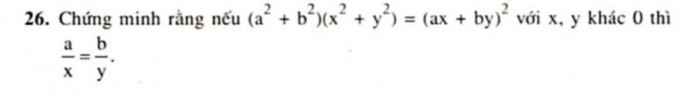
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
Đúng 1
Bình luận (0)
cho x+y=2x^5
va x^4+x^2y^2+y^4=xy(x^2+y^2)+1 tim x va y
tìm x,y tm x^2+2x^2y^2+2y^2-(x^2+y^2+2x^2)-2=0
1) \(\left\{{}\begin{matrix}xy+x+y=x^2-2y^2\\x\sqrt{2y}-y\sqrt{x-1}=2x-2y\end{matrix}\right.\)
2) \(\left\{{}\begin{matrix}2x^2+y^2-3xy+3x-2y+1=0\\4x^2-y^2+x+4=\sqrt{2x+y}+\sqrt{x+4y}\end{matrix}\right.\)


