Tam giác ABC đều có cạnh là a. Tính độ dài ba đường thẳng trung tuyến theo a.
TN
Những câu hỏi liên quan
Tam giác ABC đều có cạnh là a. Tính độ dài 3 đuờng trung tuyến theo a.
Cho tam giác ABC có độ dài các cạnh AB , BC ,AC ( theo đơn vị cm ) là ba số tự nhiên liên tiếp tăng dần có đường cao AH , đường trung tuyến AM. Tính độ dài đoạn thẳng HM ( theo đơn vị cm )
Cho tam giác ABC có độ dài ba đường trung tuyến 15,18,27.
A,Tính a²+b²+c²
B,Tính độ dài các cạnh
Xem chi tiết
a, Giả sử \(m_a=15;m_b=18;m_c=27\)
Theo công thức trung tuyến:
\(\dfrac{2b^2+2c^2-a^2}{4}=m_a\left(1\right)\)
\(\dfrac{2c^2+2a^2-b^2}{4}=m_b\)
\(\dfrac{2a^2+2b^2-c^2}{4}=m_c\)
Cộng vế theo vế các đẳng thức trên:
\(\dfrac{3\left(a^2+b^2+c^2\right)}{4}=m_a+m_b+m_c=60\)
\(\Rightarrow a^2+b^2+c^2=80\)
b, \(a^2+b^2+c^2=80\Rightarrow b^2+c^2=80-a^2\)
Khi đó \(\left(1\right)\) tương đương:
\(\dfrac{2\left(80-a^2\right)-a^2}{4}=15\)
\(\Rightarrow a=\dfrac{10\sqrt{3}}{3}\)
Tương tự ta được \(b=\dfrac{2\sqrt{66}}{3};c=\dfrac{2\sqrt{39}}{13}\)
Vậy độ dài các cạnh lần lượt là \(\dfrac{10\sqrt{3}}{3};\dfrac{2\sqrt{66}}{3};\dfrac{2\sqrt{39}}{13}\)
Đúng 1
Bình luận (0)
a, Tính độ dài đường cao và diện tích của tam giác theo 3 cạnh tam giác đó
b, Tính độ dài ba đường trung tuyến theo 3 cạnh tam giác đó
Cho tam giác đều ABC có cạnh bằng 6cm. Một điểm M nằm trên cạnh BC sao cho BM = 2cm.
a, Tính độ dài của đoạn thẳng AM và tính côsin của góc BAM ;
b, Tính bán kính đường tròn ngoại tiếp tam giác ABM;
c, Tính độ dài đường trung tuyến vẽ từ đỉnh C của tam giác ACM;
d, Tính diện tích tam giác ABM.
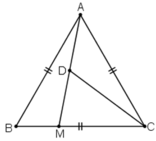
a) Do tam giác ABC là tam giác đều nên 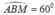 .
.
Theo định lý côsin trong tam giác ABM ta có:

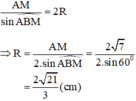
b) Theo định lý sin trong tam giác ABM ta có:
c) Ta có: BM + MC = BC nên MC = BC – BM = 6 - 2 = 4 cm.
Gọi D là trung điểm AM.
Áp dụng công thức độ dài đường trung tuyến trong tam giác ta có:
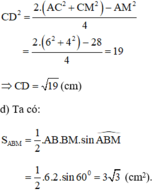
Đúng 0
Bình luận (0)
Tính độ dài đường trung tuyến
Cho tam giác ABC, có cạnh BC=a, AC=b, AB =c. Gọi ma , mb , mc lần lượt là độ dài trung tuyến từ đỉnh A, B, C của tam giác. Hãy tính ma , mb , mc theo a, b, c.
cho tam giác ABC cân tại A, M là trung điểm của BC. CMR: a, tam giác AMB= tam giác AMC. b, tính độ dài AM biết AB=10cm; BC=12cm c, kẻ đường trung tuyến CE cắt AM tại D. gọi I là điểm cách đều 3 cạnh của tam giác ABC. CMR: I;D;M thẳng hàng.
a: Xet ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Ta có: ΔABC cân tại A
mà AM là trung tuyến
nên AM là đường cao
BC=12cm nên BM=6cm
=>AM=8(cm)
c: I cách đều ba cạnh nên I là giao điểm của ba đường phân giác
=>AI là phân giác của góc BAC
mà AM là phân giác của góc BC
nên A,I,M thẳng hàng
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông tại A có D,E theo thứ tự là trung điểm của AB bà AC, đường trung tuyến AM Khi DE=5cm
a) Tính độ dài cạnh BC
b) Tính đôn dài đoạn thẳng MN
Chứng minh rằng: Điểm cách đều ba đỉnh của một tam giác vuông là trung điểm của cạnh huyền của tam giác đó.
Từ đó hãy tính độ dài đường trung tuyến xuất phát từ đỉnh góc vuông theo độ dài cạnh huyền của một tam giác vuông.
bài 66 trang 49 sách bài tập toán lớp 7
Đúng 0
Bình luận (0)



