cho 2 tam giác ABC và DEF có các góc đều nhọn và có: góc ABC=góc DEF ;góc BAC =góc EDF;AB=3.DE....chứng minh rằng bán kình đường trong ngoại tiếp tam giác ABC=3 lần bán kính đường trong ngoại tiếp tam giác DEF...
ST
Những câu hỏi liên quan
cho tam giác abc & def cs các góc đều nhọn và cs góc abc=def; bac=edf; ab=3.de... chứng minh rằng bán kính đường tròn ngoại tiếp tam giác def...
Cho tam giác ABC vuông ở A và tam giác DEF vuông ở D có AB = DE và góc ABC = góc DEF. Chứng minh tam giác ABC = tam giác DEF.
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
Đúng 0
Bình luận (0)
xét 2 tam giác vuông ABC và tam giác EDF, ta có:
cạnh góc vuông : AB = DE
góc nhọn : ABC = DEF
=> tam giác ABC = tam giác DEF ( cgv - gn )
Lý thuyết : Cạnh góc vuông - góc nhọn: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông
và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác đó bằng nhau (cgv-gn)
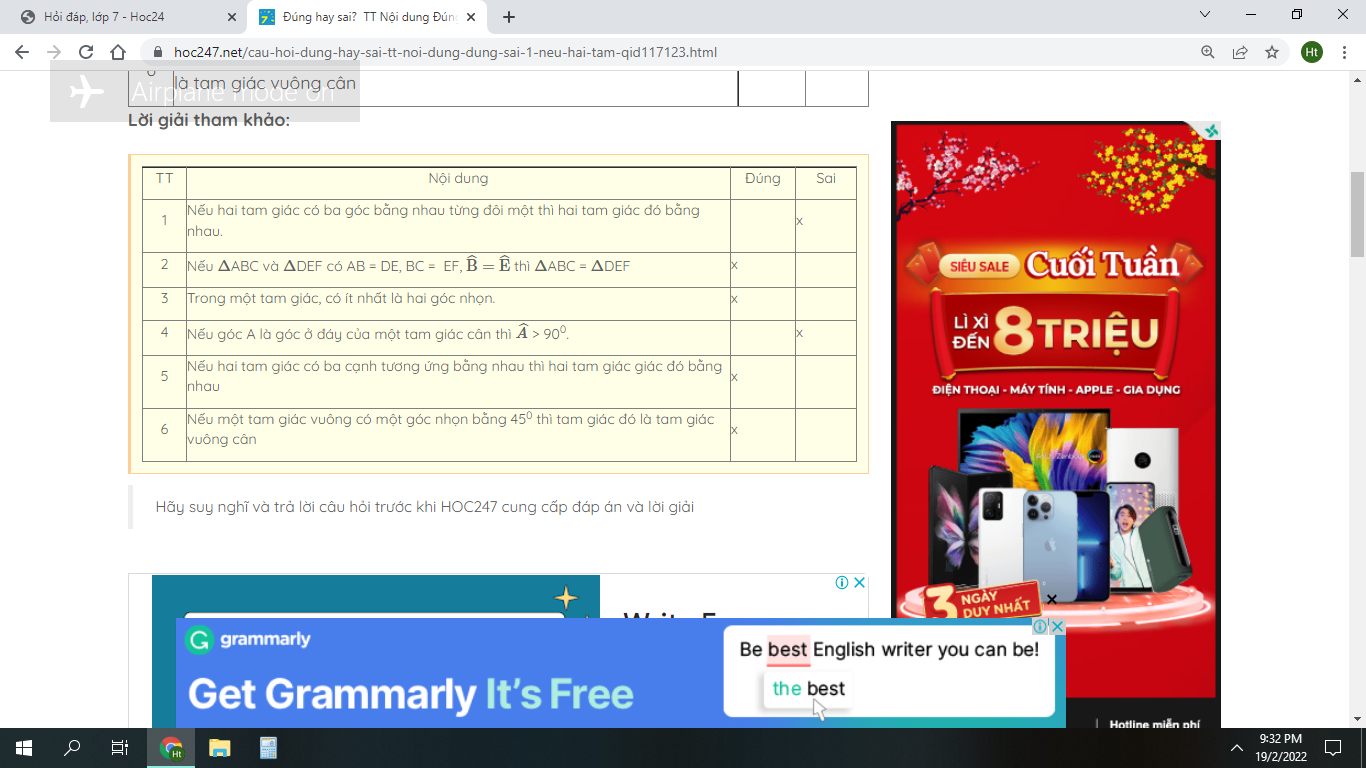
Bài 2: Đúng hay sai?TTNội dungĐúngSai1Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau. 2Nếu ABC và DEF có AB DE, BC EF, thì ABC DEF 3Trong một tam giác, có ít nhất là hai góc nhọn. 4Nếu góc A là góc ở đáy của một tam giác cân thì 900. 5Nếu hai tam giác có ba cạnh tương ứng bằng nhau thì hai tam giác giác đó bằng nhau 6Nếu một tam giác vuông có một góc nhọn bằng 450 thì tam giác đó là tam giác vuông cân
Đọc tiếp
Bài 2: Đúng hay sai?
TT | Nội dung | Đúng | Sai |
1 | Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau. |
|
|
2 | Nếu ABC và DEF có AB = DE, BC = EF, thì ABC = DEF |
|
|
3 | Trong một tam giác, có ít nhất là hai góc nhọn. |
|
|
4 | Nếu góc A là góc ở đáy của một tam giác cân thì > 900. |
|
|
5 | Nếu hai tam giác có ba cạnh tương ứng bằng nhau thì hai tam giác giác đó bằng nhau |
|
|
6 | Nếu một tam giác vuông có một góc nhọn bằng 450 thì tam giác đó là tam giác vuông cân |
|
|
1: S
2: S
3: Đ
4: S
5: Đ
6: Đ
Đúng 0
Bình luận (0)
TT | Nội dung | Đúng | Sai |
1 | Nếu hai tam giác có ba góc bằng nhau từng đôi một thì hai tam giác đó bằng nhau. |
| x |
2 | Nếu ABC và DEF có AB = DE, BC = EF, thì ABC = DEF | x |
|
3 | Trong một tam giác, có ít nhất là hai góc nhọn. | x |
|
4 | Nếu góc A là góc ở đáy của một tam giác cân thì > 900. |
| x |
5 | Nếu hai tam giác có ba cạnh tương ứng bằng nhau thì hai tam giác giác đó bằng nhau | x |
|
6 | Nếu một tam giác vuông có một góc nhọn bằng 450 thì tam giác đó là tam giác vuông cân Đúng |
Chúc em học giỏi
Đúng 0
Bình luận (1)
Cho hai tam giác ABC và DEF có các góc đều nhọn và có :
\(\widehat{ABC}=\widehat{DEF}\), \(\widehat{BAC}=\widehat{EDF}\) , \(AB=3DE\)
Chứng minh rằng bán kính đường tròn ngoại tiếp tam giác ABC bằng 3 lần bán kính đường tròn ngoại tiếp tam giác DEF
Đề thi tuyển sinh vào 10 ptnk Hồ Chí Minh 2000-2001
https://text.123doc.org/document/1812116-de-thi-vao-chuyen-toan-10.htm
Bạn vào đây nhé :D
Cho tam giác ABC và tam giác DEF có góc A = 50o , góc E=70o,góc F= 60ocạnh AB=DE , AC=DF. CM tam giác ABC= tam giác DEF
\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)
\(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)
\(Xét\) \(\Delta ABCvà\Delta DEFcó\)
\(\widehat{A}=\widehat{D}\left(=50^0\right)\)
AB=DE
AC=DF
\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)
Vậy \(\Delta ABC=\Delta DEF\)
Đúng 1
Bình luận (0)
Câu 1: Tam giác DEF vuông tại D có tổng hai góc nhọn E và F bằng : ......
Câu 2: Cho tam giác ABC có AB=AC , M là trung điểm của BC thì ta có 2 tam giác bằng nhau là : .....
Câu 3: Cho tam giác ABC và tam giác MNP có AB =MN , góc A = góc M . Để tam giác ABC = tam giác MNP thao trường hợp (c.g.c) thì cần thêm điều kiện là:....
câu 1 E + F = 90 độ
câu 2 góc AMB và góc AMC
câu 3 AC = MP
Đúng 0
Bình luận (0)
Bài 53 : Cho tam giác ABC và tam giác DEF có AB = DE , AC = DF , góc BAC = góc EDF . BI và EJ lần lượt là đường phân giác của tam giác ABC và tam giác DEF. Chứng minh :
1) Góc ABC = góc DEF
2) Góc ABI = góc DEJ
help me !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Cho △ABC=△DEF. Biết hai tia phân giác trong của góc B và góc C cắt nhau tại O tạo thành góc BOC có số đo bằng 135 độ và góc B=2 góc C Tính các góc của tam giác DEF.
cho tam giác ABC có ba góc nhọn, các đường cao AD,BE,CF gặp nhau tại H. Đường thẳng vuông góc với AB tại B và đường thẳng vuông góc với AC tại C cắt nhau tại G .
a) tam giac ABC đồng dạng với tam giác AEF
b)góc BDF = góc CDE
c) H cách đều các cạnh của tam giác DEF