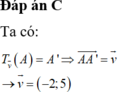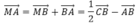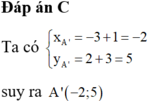Phép tịnh tiến theo vecto v=(a;b) biến đường thẳng d: x+y+1=0 thành đường thẳng d': x+y+10=0. Giá trị nhỏ nhất của biểu thức a2+b2 bằng bao nhiêu
PN
Những câu hỏi liên quan
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto
v
→
biến điểm A(3;-1) thành điểm A(1;4). Tìm tọa độ của vecto
v
→
? A.
v
→
(-4;3) B.
v
→
(4;3) C.
v
→
(-2;5) D.
v
→
(5;-2)
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → biến điểm A(3;-1) thành điểm A'(1;4). Tìm tọa độ của vecto v → ?
A. v → =(-4;3)
B. v → =(4;3)
C. v → =(-2;5)
D. v → =(5;-2)
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto
v
→
biến điểm
A
3
;
−
1
thành điểm
A
1
;
4
Tìm tọa độ của vecto ? A.
v
→
−
4
;...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → biến điểm A 3 ; − 1 thành điểm A ' 1 ; 4 Tìm tọa độ của vecto ?
A. v → = − 4 ; 3
B. v → = 4 ; 3
C. v → = − 2 ; 5
D. v → = 5 ; − 2
Đáp án C
Ta có:
T v → A = A ' ⇒ A A ' → = v → → v → = − 2 ; 5
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ
v
→
-
1
;
2
,
A
3
;
5
,
B
-
1
;
1
và đường thẳng d có phương trình
x
–
2...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho vectơ v → = - 1 ; 2 , A 3 ; 5 , B - 1 ; 1 và đường thẳng d có phương trình x – 2 y + 3 = 0 .
a. Tìm tọa độ của các điểm A' , B' theo thứ tự là ảnh của A, B qua phép tịnh tiến theo vecto v →
b. Tìm tọa độ của điểm C sao cho A là ảnh của C qua phép tịnh tiến theo vectơ v →
c. Tìm phương trình của đường thẳng d' là ảnh của d qua phép tịnh tiến theo v .
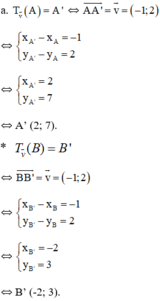
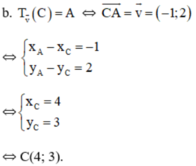
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0
Đúng 0
Bình luận (0)
Cho điểm M(-4;2) và vecto v =(3;-1). Tìm điểm N biết M là ảnh của N qua phép tịnh tiến theo vecto v.
\(T_{\overrightarrow{v}}\left(N\right)=M\Rightarrow\overrightarrow{NM}=\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x_N+3=-4\\y_N-1=2\end{matrix}\right.\) \(\Rightarrow N\left(-7;3\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ, phép tịnh tiến theo vecto v → ( 0 ; 0 ) biến điểm A(0;2) thành điểm A’ có tọa độ:
A. A’(1;1)
B. A’(1;2)
C. A’(1;3)
D. A’(0;2)
Phép tịnh tiến theo vecto không biến mỗi điểm thành chính nó.
Đáp án D
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến theo vecto
v
→
biến M thành A thì
v
→
bằng: A.
1
2
A
D
→
+
D
C
→
B.
A
D
→
+...
Đọc tiếp
Cho hình vuông ABCD có M là trung điểm của BC. Phép tịnh tiến theo vecto v → biến M thành A thì v → bằng:

A. 1 2 A D → + D C →
B. A D → + A C →
C. 1 2 C B → - A B →
D. 1 2 C B → + A B →
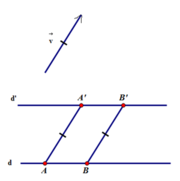
Nêu cách xác định ảnh của đường thẳng d qua phép tịnh tiến theo vecto v → .
Lấy 2 điểm A và B thuộc đường thẳng d
Lần lượt thực hiện phép tịnh tiến A, B theo vecto v→ ta được 2 điểm A’và B’
Đường thẳng đi qua 2 điểm A’ và B’là đường thẳng d’ hay d’là ảnh của đường thẳng d
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → =(-3;2) biến điểm A(1;3) thành điểm A’ có tọa độ
A. (1;3)
B. (-4;-1)
C. (-2;5)
D. (-3;5)
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → =(-3;2) biến điểm A(1;3) thành điểm A’ có tọa độ
A. (1;3)
B. (-4;-1)
C. (-2;5)
D. (-3;5)
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto
v
→
−
3
;
2
biến điểm
A
1
;
3
thành điểm A’ có tọa độ A.
1
;
3
B.
−
4...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, phép tịnh tiến theo vecto v → = − 3 ; 2 biến điểm A 1 ; 3 thành điểm A’ có tọa độ
A. 1 ; 3
B. − 4 ; − 1
C. − 2 ; 5
D. − 3 ; 5
Đáp án C
Ta có x A ' = − 3 + 1 = − 2 y A ' = 2 + 3 = 5 suy ra A ' − 2 ; 5
Đúng 0
Bình luận (0)