Cho hình chóp s ABCD có đáy hình vuông cạnh a, SA vuông góc ABCD;SA=2a
a) Chứng minh ; BC vuông góc SAD
b) Tính góc giữa SB và mặt phẳng SAD
c) tính khoảng cách từ A đến mặt phẳng SCD
d) tính khoảng cách từ B đến mặt phẳng SAC
Cho khối chóp S. ABCD có đáy ABCD là hình vuông cạnh a. Biết SA vuông góc với đáy (ABCD) và SA= a 6 . Thể tích khối chóp S. ABCD là
A. a 3 4
B. a 3 3
C. a 3 3 3
D. a 3 2 3
Cho hình chóp S. ABCD có đáy ABCD là hình thoi cạnh a A B C ^ = 60 0 , cạnh bên SA vuông góc với đáy SA = a 3 Tính thể tích của khối chóp S. ABCD
A. a 3 4
B. a 3 3 6
C. a 3 2
D. a 3 3 3
Cho hình chóp S. ABCD có đáy là hình vuông cạnh a. S A = a 2 và SA vuông góc mặt phẳng đáy. Góc giữa cạnh bên SC với đáy bằng
A. 60⁰.
B. 30⁰.
C. 45⁰.
D. 90⁰.
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh bằng 1. Cạnh bên SA vuông góc với mặt phẳng ABCD và SC = 5 . Tính thể tích khối chóp S. ABCD
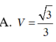
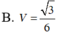
![]()
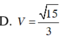
Chọn đáp án A
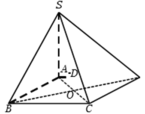
Đường chéo hình vuông AC = 2
Xét tam giác SAC, ta có
![]()
Chiều cao của khối chóp là SA = 3
Diện tích hình vuông ABCD là
![]()
Thể tích khối chóp S. ABCD là

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, SA = a 2 . Một mặt phẳng đi qua A vuông góc với SC cắt SB, SD, SC lần lượt tại B', D', C'. Thể tích khối chóp S. AB'C'D' là:
A. V = 2 a 3 3 9
B. V = 2 a 3 2 3
C. V = a 3 2 9
D. V = 2 a 3 3 3
Chọn C
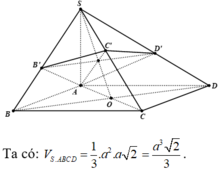
Dựa vào giả thiết ta có B', C', D' lần lượt là hình chiếu của A lên SB, SC, SD.
Tam giác SAC vuông cân tại A nên C' là trung điểm của SC.
Trong tam giác vuông SAB' ta có:
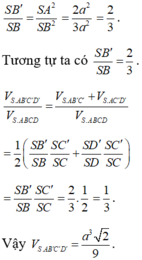

Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt đáy và S A = a 2 . Tìm số đo của góc giữa đường thẳng SC và mặt phẳng (SAB)
A. 45 °
B. 30 °
C. 90 °
D. 60 °
Cho hình chóp S(ABCD) đáy là hình vuông cạnh a SA vuông góc (ABCD) SA= a√2 a, chứng minh BD vuông góc với (SAC) b, tính góc a giữa đường SC và mặt đáy
Ta có:
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\AC\perp BD\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{a\sqrt{2}}{a\sqrt{2}}=1\)
\(\Rightarrow\widehat{SCA}=45^0\)
Cho hình chóp S. ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với mặt phẳng đáy, góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 45° và SC = 2a. Tính thể tích V của khối chóp S.ABCD.
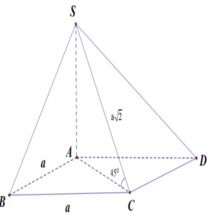
Vì SA ⊥ (ABCD) nên AC là hình chiếu vuông góc của SC lên mặt phẳng (ABCD).
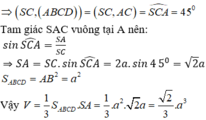
Cho khối chóp S. ABCD , có SA vuông góc với mặt đáy ABCD , SA = x. Mặt đáy là hình chữ nhật ABCD có cạnh là 4x. và 3x . Tính khối chóp S. ABCD.
\(V=\dfrac{1}{3}SA.AB.AD=\dfrac{1}{3}.x.4x.3x=4x^3\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh bên SA vuông góc với đáy (ABCD) và SA =a 3 . Khi đó, thể tích của khối chóp bằng:
A. a 3 3 3
B. a 3 3 4
C. a 3 3
D. a 3 3 6