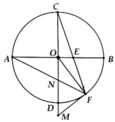
Cho AB và CD là hai đường kính vuông góc của(O;R). Trên tia đối của CO lấy điểm S. SA cắt (O) tại M. Tiếp tuyến tại M với (O) cắt CD tại E, BM cắt CD tại F. a) c/m EA. AM=MF.OA
b) SB cắt (O) tại I. c/m A,I,F thẳng hàng
c) Giả sử EM=R. Tính FA.SM theo R
d) kẻ MH vuông góc với AB tại H. xác định vị trí điểm S để diện tích tam giác MHD lớn nhất