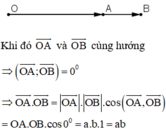
Cho điểm A nằm ngoài (O;R), từ A kẻ các tiếp tuyến AB, AC, cát tuyến AMN
a, Chứng minh ABOC nội tiếp
b, AM.AN = AB^2
c, Tiếp tuyến tại N của (O) cắt BC tại F.Chứng minh FM là tiếp tuyến của (O;R)
d, Gọi P là giao điểm của dây BC và dây MN, E là giao điểm của đường tròn ngoại tiếp tam giác MNO và đường tròn ngoại tiếp tứ giác ABOC. Chứng minh P,E,O thẳng hàng


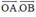 trong hai trường hợp:
trong hai trường hợp: