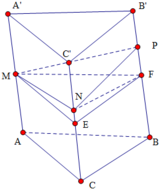
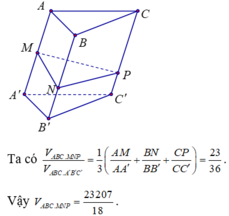
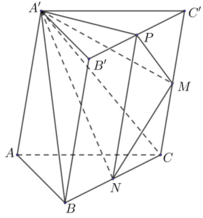
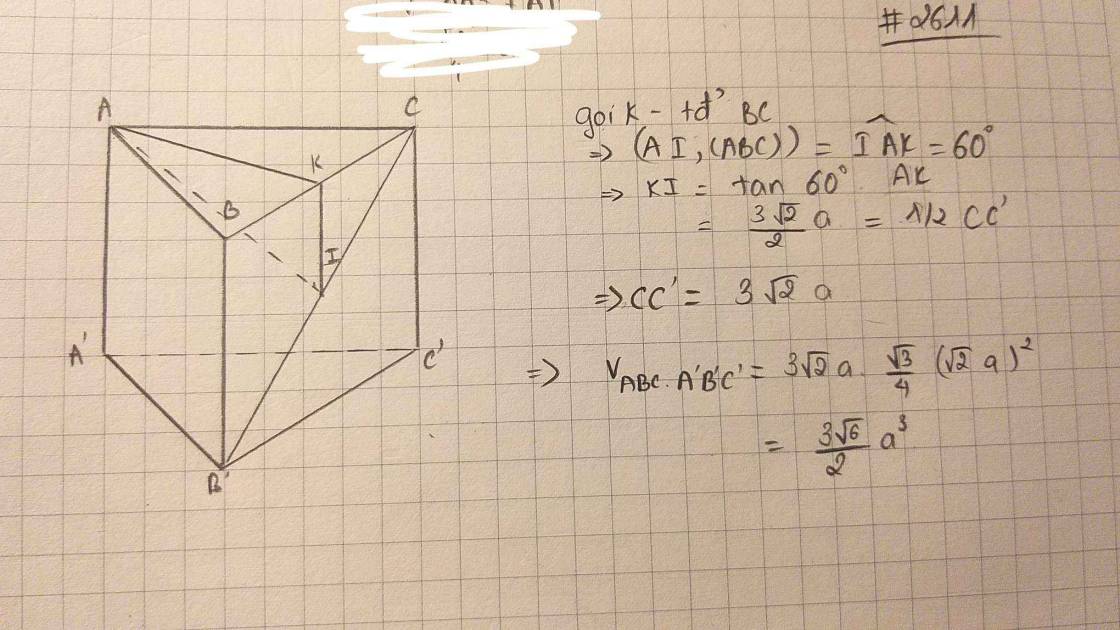
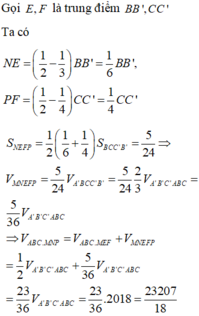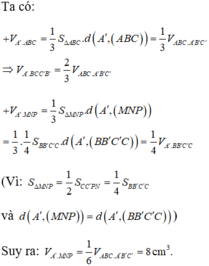cho khối lăng trụ ABCA'B'C' có thể tích bằng 2018.Gọi M là trung điểm của AA'N,P lần lượt là các điểm nằm trên các cạnh BB',CC' , sao cho BN=2B'N , CP=3C'P. Tính thể tích khối đa diện ABCMNP.
HT
Những câu hỏi liên quan
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 2018. Gọi M là trung điểm AA’; N, P lần lượt là các điểm nằm trên các cạnh BB’, CC’ sao cho
B
N
2
B
N
,
C
P
3
C
P
.
Tính thể tích khối đa diện ABCMNP A.
4036
3
B.
32288
27
C.
4...
Đọc tiếp
Cho khối lăng trụ ABC.A’B’C’ có thể tích bằng 2018. Gọi M là trung điểm AA’; N, P lần lượt là các điểm nằm trên các cạnh BB’, CC’ sao cho B N = 2 B ' N , C P = 3 C ' P . Tính thể tích khối đa diện ABCMNP
A. 4036 3
B. 32288 27
C. 40360 27
D. 23207 18
Cho khối lăng trụ ABC. ABC có thể tích bằng 2018. Gọi M là trung điểm AA ; N, P lần lượt là các điểm nằm trên các cạnh BB, CC sao cho BN2BN, CP3CP. Tính thể tích khối đa diện ABC. MNP. A.
32288
27
B.
40360
27
C.
4036
3
D.
23207
18
Đọc tiếp
Cho khối lăng trụ ABC. A'B'C' có thể tích bằng 2018. Gọi M là trung điểm AA' ; N, P lần lượt là các điểm nằm trên các cạnh BB', CC' sao cho BN=2B'N, CP=3C'P. Tính thể tích khối đa diện ABC. MNP.
A. 32288 27
B. 40360 27
C. 4036 3
D. 23207 18
Cho hình lăng trụ ABC.ABC có thể tích bằng 48cm3. Gọi M, N, P theo thứ tự là trung điểm các cạnh CC, BC và BC, khi đó thể tích V của khối chóp A.MNP là: A.16/3 cm3 B.8cm3 C.24cm3 D. 12cm3
Đọc tiếp
Cho hình lăng trụ ABC.A'B'C' có thể tích bằng 48cm3. Gọi M, N, P theo thứ tự là trung điểm các cạnh CC', BC và B'C', khi đó thể tích V của khối chóp A'.MNP là:
A.16/3 cm3
B.8cm3
C.24cm3
D. 12cm3
Cho lăng trụ đứng tam giác ABC.A'B'C' có đáy ABC là tam giác vuông, AB=BC=a, cạnh bên \(AA'=a\sqrt{2}\). Gọi M là trung điểm cạnh BC. Tính theo a thể tích của khối lăng trụ ABC.A'B'C' và khoảng cách giữa 2 đường thẳng AM, B'C
Từ giả thiết ta suy ra tam giác ABC là tam giác vuông cân tại B
Thể tích của khối lăng trụ là \(V_{ABC.A'B'C'}=AA'.BC=a\sqrt{2.}\frac{1}{2}a^2=\frac{\sqrt{2}}{2}a^3\)
Gọi E là trung điểm của BB'. Khi đó mặt phẳng (AME) song song với B'C nên khoảng cách giữa 2 đường thẳng AM, B'C bằng khoảng cách giữa B'C và mặt phẳng (AME)
Nhận thấy, khoảng cách từ B đến mặt phẳng (AME) bằng khoảng cách từ C đến mặt phẳng (AME)
Gọi h là khoảng cách từ B đến mặt phẳng (AME). Do đó tứ diện BAME có BA, BM, BE đôi một vuông góc với nhau nên :
\(\frac{1}{h^2}=\frac{1}{BA^2}+\frac{1}{BM^2}+\frac{1}{BE^2}\Rightarrow\frac{1}{h^2}=\frac{1}{a^2}+\frac{4}{a^2}+\frac{2}{a^2}=\frac{7}{a^2}\)
\(\Rightarrow h=\frac{a\sqrt{7}}{7}\)
Vậy khoảng cách giữa 2 đường thẳng B'C và AM bằng \(\frac{a\sqrt{7}}{7}\)
Đúng 0
Bình luận (0)
Cho hình lăng trụ đứng ABC.A'B'C' có đáy là tam giác đều cạnh a√2 . Gọi I là trung điểm B'C góc giữa AI và đáy bằng 60. Tính thể tích V của khối lăng trụ ABC. A'B'C' .
1.cho khối lăng trụ tam giác ABC.A'B'C'. Gọi I,J,K lần lượt là trung điểm của AB,AA',B'C' . Mặt phẳng (IJK) chia khối lăng trụ thành 2 phần.Tính tỉ số thể tích của 2 phần đó.
2.Cho khối tứ diện ABCD có cạnh AB>1,các cạnh còn lại có độ dài không lớn hơn 1. Gọi V là thể tích của khối tứ diện. Tìm giá trị lớn nhất của V.
Cho lăng trụ ABCA′B′C′, đáy là tam giác đều cạnh bằng a, tứ giác ABB′A′ là hình thoi,
A
AC
^
60
o
,
B
C
a
3
2
. Tính thể tích lăng trụ ABCA′B′C′. A.
3...
Đọc tiếp
Cho lăng trụ ABCA′B′C′, đáy là tam giác đều cạnh bằng a, tứ giác ABB′A′ là hình thoi, A ' AC ^ = 60 o , B ' C = a 3 2 . Tính thể tích lăng trụ ABCA′B′C′.
A. 3 a 3 4
B. 3 3 a 3 4
C. 3 3 a 3 16
D. 3 a 3 16
Đáp án A
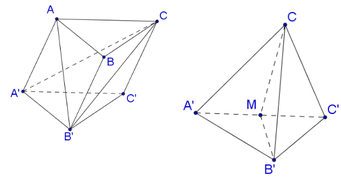
Dễ dàng tính được các cạnh của tứ diện CA′B′C′:
A ' C = A ' C ' = CC ' = B ' C ' = A ' B ' = a .
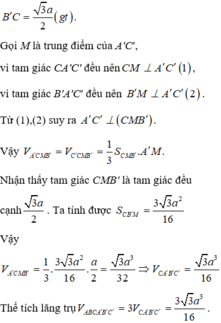
Đúng 0
Bình luận (0)
Cho lăng trụ đều ABC.A'B'C' có AB = a và đường thẳng A'B tạo với đáy một góc bằng 60 độ. Gọi M và N lần lượt là trung điểm của các cạnh AC và B'C'. Tính theo a thể tích củ khối lăng trụ ABC.A'B'C' và độ dài của MN
\(AA'\perp\left(ABC\right)\Rightarrow\widehat{A'BA}\) là góc giữa A'B với đáy
Suy ra : \(\widehat{A'BA}=60^o\Rightarrow AA'=AB.\tan\widehat{A'BA}=a\sqrt{3}\)
Do đó \(V_{ABC.A'B'C'}=AA'.S_{\Delta ABC}=\frac{3a^2}{4}\)
Gọi K là trung điểm cạnh BC, suy ra Tam giác MNK vuông tại K, có :
\(MK=\frac{AB}{2}=\frac{a}{2};NK=AA'=a\sqrt{3}\)
Do đó : \(MN=\sqrt{MK^2+NK^2}=\frac{a\sqrt{13}}{2}\)
Đúng 0
Bình luận (0)
Cho lăng trụ đứng tam giác
A
B
C
.
A
B
C
.
Gọi M, N, P, Q là các điểm thuộc các cạnh
A
A
,
B
B
,
C
C
,
B
C
thỏa mãn
A
M
A
A...
Đọc tiếp
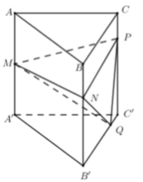
Cho lăng trụ đứng tam giác A B C . A ' B ' C ' . Gọi M, N, P, Q là các điểm thuộc các cạnh A A ' , B B ' , C C ' , B ' C ' thỏa mãn A M A A ' = 1 2 , B N B B ' = 1 3 , C P C C ' = 1 4 , C ' Q C ' B ' = 1 5 . Gọi V 1 , V 2 lần lượt là thể tích khối tứ diện MNPQ và khối lăng trụ A B C . A ' B ' C ' . Tính tỷ số V 1 V 2 .
A. V 1 V 2 = 11 30
B. V 1 V 2 = 11 45
C. V 1 V 2 = 19 45
D. V 1 V 2 = 22 45
Chọn B.
Phương pháp:
+) Sử dụng công thức tính thể tích
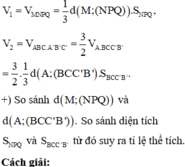
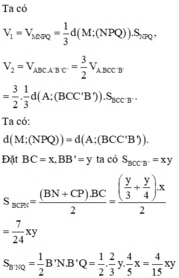
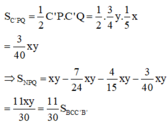
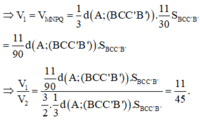
Đúng 0
Bình luận (0)