Cho tam giác ABC vuông tại A, đường cao AH. Lấy điểm K bất kỳ trên cạnh AC \(\left(K\ne A;K\ne C\right)\). Gọi D là hình chiếu của A trên BK. Chứng minh \(S_{BHD}=\dfrac{1}{4}S_{BKC}.cos^2\widehat{ABD}\)
H24
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AH là đường cao. Trên tia đối của tia AC lấy điểm E bất kỳ. Gọi K là hình chiếu của A trên BE. Chứng minh góc BKH = góc BCA.
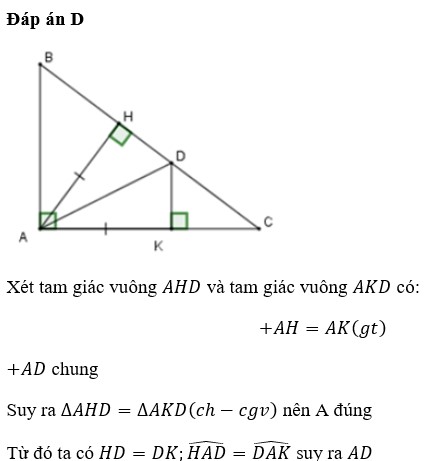
Cho tam giác ABC vuông tại A , kẻ đường cao AH . trên cạnh AC lấy điểm K sao cho AK = AH . kẻ KD vuông góc với AC tại K ( D thuộc BC ) > chứng minh
a, tam giác AHD = tam giác AKD
b, AD là đường trung trực của đoạn thẳng AK
a: Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AH=AK
AD chung
=>ΔAHD=ΔAKD
b: AK=AH
DH=DK
=>AD là trung trực của HK
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Trên cạnh AC lấy điểm K sao cho AKAH. Kẻ KD vuông góc với AC. Chọn câu đúng A. Tam giác AHD tam giác AKD B. AD là đường trung trực của đoạn thẳng HK C. AD là tia phân giác của góc HAK D. Cả A, B, C đều đúng
Đọc tiếp
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Trên cạnh AC lấy điểm K sao cho AK=AH. Kẻ KD vuông góc với AC. Chọn câu đúng
A. Tam giác AHD= tam giác AKD
B. AD là đường trung trực của đoạn thẳng HK
C. AD là tia phân giác của góc HAK
D. Cả A, B, C đều đúng
cho tam giác ABC cân tại A, đường cao AH. trên cạnh AB lấy điểm D bất kỳ . Kẻ DE song song với AH. Trên HC lấy điểm F sao cho HE = CF, kẻ đường thẳng qua C vuông góc với AC cắt AH tại G. chứng minh DFG=90
cho tam giác ABC vuông tại A có đường cao AH. lấy M bất kỳ trên cạnh BC trên nửa mặt phẳng bờ BC có chứa A kẻ tia Bx, Cy vuông góc với BC đường thẳng vuông góc với AM tại A cắt By, Cy lần lượt tại I và K. Chứng minh:
a) \(AB^2\)=BH.BC
b) tam giác ACK đồng dạng tam giác ABM
c) tam giác ABC đồng dạng tam giác AMK
Vẽ hình nữa nhé!!!
BÀI TOÁN LỚP 7 CHO TAM GIÁC VUÔNG TẠI A CÓ ĐƯỜNG CAO AH, TRÊN AC LẤY MỘT ĐIỂM K BẤT KỲ. GỌI D LÀ HÌNH CHIẾU CỦA A TRÊN BK. CHỨNG MINH GÓC BDH BẰNG GÓC C
Cho tam giác ABC vuông cân tại A, AH là đường cao . Gọi M là điểm bất kì trên cạnh BC . Gọi I , K lần lượt là hình chiếu của M trên cạnh AB , AC . Chứng minh tam giác IHK vuông cân
Cho tam giác ABC vuông tại A, đường cao AH, biết BC=8cm, AB=4cm.
a) Giải tam giác vuông ABC
b) Tính AH,BH,HC
c) Trên cạnh AC lấy điểm K (K khác A, K khác C). Gọi D là hình chiếu của A trên BK. Chứng minh BD.BK=BH.BC
Cho tam giác ABC vuông tại A, kẻ đường cao AH . trên cạnh AC lấy điểm K sao cho AK=AH. Kẻ KD vuông góc với AC tại K (D thuộc BC) chứng minh
a) tam giác AHD = tam giác AKD
b) AD là đường trung trực của đoạn thẳng HK
GiẢI:
VẼ DG vuông góc vối AH (G thuộc AH). Suy ra: DG//BC.
Ta có:
Góc BAH = góc BCA ( cùng phụ góc B)
Mà góc BCA = góc GDA (góc trong cùng phía)
Do đó: góc BAH = góc GDA
Xét hai tam giác ABH và DAG, ta có:
ü góc BAH = góc GDA (chứng minh trên)
ü AB=AD ( giả thuyết)
ü ABH vuông tại H, và AHG vuông tại G.
Nếu học tới các trường hợp bằng nhau của tam giác vuông thì ghi là:
Tam giác ABH = tam giác DAG (cạnh huyền góc nhon)
Nếu chưa học tới thì ghi:
Tam giác ABH = tam giác DAG (góc cạnh góc)
Suy ra: AH=DG
Lại có: DG=HE (vì EDGH là hình chủ nhật)
Vậy AH=HE