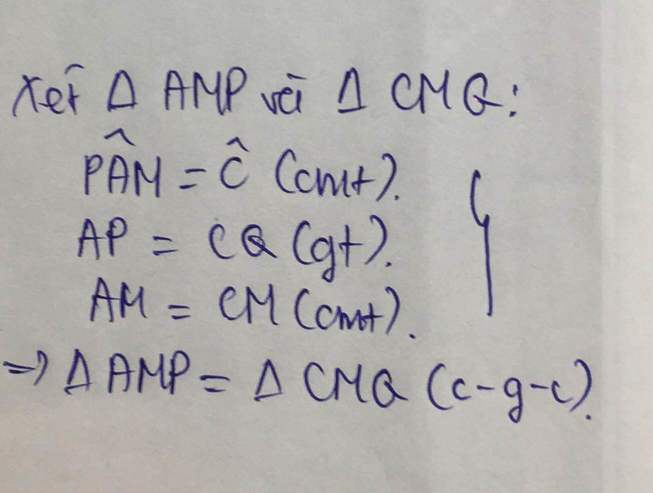tam giác ABC vuông cân tại A, AB=a ko đổi . Lấy D thuộc AB;E thuộc AC sao cho AD=CE. TÌm SBCED min
KR
Những câu hỏi liên quan
Cho tam giác ABC cân tại A, có BC=2a. M là trung điểm BC. Lấy 2 diểm D và E theo thứ tự thuộc các cạnh AB, AC sao cho góc DME ko đổi
a. CMR BD.CE ko đổi
b. CMR CM là phân giác BCE
c. Cho tam giác ABC đều, CMR chu vi tam giác ADE ko đổi
cho tam giác ABC cân tại A ( A < 90 độ ) . Kẻ BD vuông góc Ac ( D thuộc AC ) , CE vuông góc AB ( E thuộc AB ) , BD và CE cắt nhau tại H . a, CM : BD = CE . b, CM : tam giác BHC cân . c, CM : AH là đường trung trực của BC . d, TRên tia BD lấy điểm K sao cho D là trung điểm của BK . So sánh ECB và DKC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
góc BAD chung
=>ΔADB=ΔAEC
=>BD=CE
b: góc ABD=góc ACE
=>góc HBC=góc HCB
=>ΔHBC cân tại H
c: AB=AC
HB=HC
=>AH là trung trực của BC
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = AC . Lấy điểm D thuộc cạnh AB , điểm E thuộc cạnh AC sao cho AD = AE . Đường thẳng đi qua D và vuông góc với BE cắt CA tại K. Chứng minh tam giác KDC là tam giác cân.
Bài 1: Cho tam giác ABC cân tại A. Lấy D, E thuộc BC sao cho BD = CF. CMR: tam giác ABC cân tại A.
Bài 2: Tam giác ABC cân tại A. Lấy M thuộc AB, N thuộc AC sao cho AM = AN.
a) CMR: MN//BC.
b) Cho CM cắt BN tại I. CMR: IB = IC.
Bài 3: Tam giác ABC cân tại A. Lấy M thuộc BC. Vẽ MK//AB (K thuộc AC). CMR: MK = KC.
Cho tam giác ABC cân tại A (góc A < 90 độ).Kẻ BM vuông tại AC (M thuộc AC) , CD vuông tại AB (D thuộc AB). BM và CD cắt nhau tại E.
a, Chứng minh tam giác BDC = tam giác CMD
b, Chứng minh tam giác BCE cân
a. Xét \(2\Delta:\Delta BDC\) và \(\Delta CMD\) có:
\(\left\{{}\begin{matrix}\widehat{B}=\widehat{C}\left(gt\right)\\BC.chung\end{matrix}\right.\)
\(\Rightarrow\Delta BDC=\Delta CMD\) (cạnh huyền - góc nhọn)
b. Vì \(\Delta BDC=\Delta CMD\) (theo câu a)
\(\Rightarrow\widehat{DCB}=\widehat{MBC}\) (2 góc tương ứng)
\(\Rightarrow\Delta BCE\) cân tại E
Đúng 3
Bình luận (0)
Cho tam giác ABC vuông cân tại A. Lấy điểm D thuộc nửa mặt phẳng bờ AB không chứa C sao cho tam giác DAB vuông cân tại D; điểm E (khác A) không thuộc đoạn AD. Đường thẳng qua E, vuông góc với BE cắt AC tại F. Chứng minh rằng EF=EB
Cho tam giac ABC vuông tại C có góc B=40 độ. Tia phân giác AD. Lấy E thuộc AB sao cho AE=AC.
a) So sánh các cạnh của tam giác ABC.
b) Chứng tỏ tam giác AED vuông.
c) Đường vuông góc với AC tại A cắt đường thẳng DE tại H. Chứng minh tam giác ADH cân.
d) Kẻ CK vuông góc AB tại K. Lấy I thuộc AB sao cho BI=BC. Chứng minh: CI là phân giác ACK.
cho tam giác abc vuông cân tại a lấy p thuộc ab lấy q thuộc ac sao cho ap=cq. m là trung điểm bc a, c/m tam giác amp=cmq b,c/m tam giác mpq vuông cân
Cho Tam Giác ABC cân tại A . Lấy M bất kì trên đáy BC . kẻ MN vuông govs AB, MQ vuông góc AC, BH vuông góc AC, MI vuông góc BH. CHứng minh: a) tam giác NBM=Tam giác IMB ; b)) MQ=IH c)MN+MQ ko đổi
Ai trả lời giúp tôi với ple