Cho tam giác ABC vuông ở A,có AB=5cm;BC=13cm.Ba đừng trung tuyến AM,BN,CE cắt nhau tại O.Tính độ dài AM,BN,CE
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NK
Những câu hỏi liên quan
cho tam giác abc vuông tại a có ab=3cm ac=5cm đường phân giác ad . đường vuông góc dc cắt ac ở ea, tam giác abc đồng dạng tam giác becb, tính bc, bd,ad
Xem chi tiết
a:
Sửa đề tam giác DEC
Xet ΔABC vuông tại A và ΔDEC vuông tại D có
góc C chung
=>ΔABC đồng dạng với ΔDEC
b: \(BC=\sqrt{3^2+5^2}=\sqrt{34}\left(cm\right)\)
\(AD=\dfrac{2\cdot3\cdot5}{3+5}\cdot cos45=\dfrac{15\sqrt{2}}{8}\left(cm\right)\)
AD là phân giác
=>BD/AB=CD/AC
=>\(\dfrac{BD}{3}=\dfrac{CD}{5}=\dfrac{\sqrt{34}}{8}\)
=>\(BD=\dfrac{3\sqrt{34}}{8}\left(cm\right)\)
Đúng 0
Bình luận (0)
a)Cho tam giác ABC vuông tại A, biết AB=4cm; BC=5cm, Tonhs cosC+TanB
b) Cho tam giác ABC vuông tại A, có AB=5cm,BC=10cm. Tính sinC và số đo góc B
c) Cho tam giác ABC vuông tại A, biết cosB=8cm. hãy tính các tỉ số lượng giác của góc C. E c.ơn ạ!
Câu a) với b) tính cos, tan, sin là tính góc hay cạnh vậy cậu?
Đúng 0
Bình luận (9)
a) Xét \(\Delta ABC\) vuông tại `A`
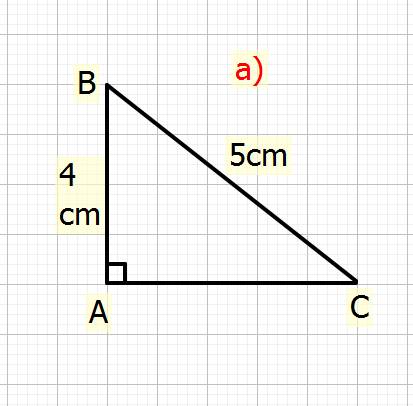
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow5^2=4^2+AC^2\\ \Rightarrow AC^2=5^2-4^2\\ \Rightarrow AC^2=25-16=9\\ \Rightarrow AC=\sqrt{9}=3cm\)
Vậy: \(AC=3cm\)
Ta có: \(CosC=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow CosC=\dfrac{3}{5}\\ \Rightarrow CosC\approx53^o\)
Vậy: Góc C khoảng \(53^o\)
Ta có: \(TanB=\dfrac{AC}{AB}\left(tslg\right)\)
\(\Rightarrow TanB=\dfrac{3}{4}\\ \Rightarrow TanB\approx37^o\)
Vậy: Góc B khoảng \(37^o\)
_
b) Xét \(\Delta ABC\) vuông tại `A`
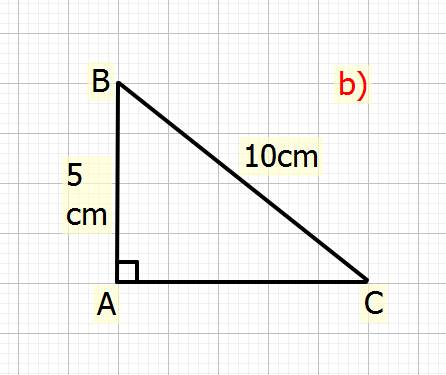
Ta có: \(BC^2=AB^2+AC^2\) (đl Pytago)
\(\Rightarrow10^2=5^2+AC^2\\ \Rightarrow AC^2=10^2-5^2\\\Rightarrow AC^2=100-25=75\\ \Rightarrow AC=\sqrt{75}=5\sqrt{3}cm\)
Vậy: \(AC=5\sqrt{3}cm\)
Ta có: \(SinC=\dfrac{AB}{BC}\left(tslg\right)\)
\(\Rightarrow SinC=\dfrac{5}{10}\\ \Rightarrow30^o\)
Vậy: Góc C là \(30^o\)
Ta có: \(SinB=\dfrac{AC}{BC}\left(tslg\right)\)
\(\Rightarrow SinB=\dfrac{5\sqrt{3}}{10}\\ \Rightarrow SinB=60^o\)
Vậy: Góc B là \(60^o\).
Đúng 1
Bình luận (2)
Cho tam giác ABC có AH vuông góc với BC .Biết AB=5cm,AC=5cm,Bc=căn50 a) Tam giác ABC có phải là tam giác vuông không ? b) Chứng minh tam giác AHC cân.Tính độ dài cạnh AH
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔAHC vuông tại H có \(\widehat{C}=45^0\)
nên ΔAHC vuông cân tại H
=>\(AH=HC=\dfrac{BC}{2}=\dfrac{5}{2}\sqrt{2}\left(cm\right)\)
Đúng 0
Bình luận (0)
BÀI TẬP
Bài 1. Cho tam giác ABC có AB=5cm; AC=7cm. So sánh <B và <C
Bài 2. Cho tam giác ABC có AB=3cm; AC= 4cm;BC = 5cm. So sánh các góc của
tam giác
Bài 3.Cho tam giác có <B=60 0 ; <C =40 0 . So sánh các cạnh của tam giác ABC
Bài 4. Cho tam giác ABC vuông ở A có AB= 6cm; BC = 10 cm
1/ Tính AC
2/ So sánh các góc của tam giác ABC
cho tam giác ABC vuông ở A có AB=5cm, BC=13cm. Kẻ AH vuông góc với BC . Tính AC, AH, HB, HC
tam giác ABC vuông ở A có AB = 5cm , AC =12cm .Bán kính đường tròn ngoại tiếp tam giác đó bằng
Xem chi tiết
\(\Delta ABC\) vuông tại A
\(\Rightarrow BC^2=AB^2+AC^2\) (Pytago)
\(=5^2+12^2\)
\(=169\)
\(\Rightarrow BC=13\left(cm\right)\)
Gọi R là bán kính cần tìm
\(\Rightarrow\) Bán kính đường tròn ngoại tiếp \(\Delta ABC\):
\(R=\dfrac{BC}{2}=\dfrac{13}{2}=6,5\left(cm\right)\)
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông ở A có AB=5cm,AC=12cm,đường cao AH với H € BC tính BH,CH,AH
Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Tam giác ABC vuông tại A
\(AB^2=BH.BC\\ \Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{5^2}{13}=\dfrac{25}{13}\left(cm\right)\)
\(AB.AC=AH.BC\\ \Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{5.12}{13}=\dfrac{60}{13}\left(cm\right)\)
\(AC^2=HC.BC\\ \Rightarrow HC=\dfrac{AC^2}{BC}=\dfrac{12^2}{13}=\dfrac{144}{13}\left(cm\right)\)
Đúng 2
Bình luận (0)
ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{5^2+12^2}=13\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=\dfrac{5^2}{13}=\dfrac{25}{13}\left(cm\right)\\CH=\dfrac{12^2}{13}=\dfrac{144}{13}\left(cm\right)\\AH=\dfrac{5\cdot12}{13}=\dfrac{60}{13}\left(cm\right)\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB\(=\) 3cm, BC \(=5cm.\)
Tính diện tích tam giác ABC
Áp dụng định lí Pytago có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(\Rightarrow S_{ABC}=\dfrac{AB.AC}{2}=\dfrac{3.4}{2}=6\left(cm^2\right)\)
Đúng 2
Bình luận (2)
Diện tích tam giác ABC là:
( 3. 5 ): 2 = 7.5 ( cm2)
Đ/s:...
Đúng 1
Bình luận (3)
Cho tam giác ABC vuông ở A và có đường cao AH,AB=5cm, AC=12cm
Tính độ dài các đoạn thẳng BC,AH
Xét tam giác ABC vuông tại A có:
AB^2+AC^2=BC^2
5^2+12^2=BC^2
=>BC^2=169
=>BC=13.
Có:SABC=1/2.AB.AC=1/2.AH.BC=1/2.5.12=30
=>1/2.AH.13=30
=>AH=60/13
Đúng 0
Bình luận (0)
1) Cho tam giác ABC vuông ở A và có đường cao AH,AB=5cm, AC=12cm
Tính độ dài các đoạn thẳng BC,AH
2)Cho tam giác ABC( góc A=90 độ), đường cao AH. chứng minh rằng AH2=BH.CH






