Tam giác ABC vuông tại A(O;AB) cắt BC tại D. Kẻ OH vuông góc với BD. Đường cao AK của tam giác ACO cắt OH tại M a) Chứng minh OH.OM= OK.OC b) Chứng minh MD là tiếp tuyến của đường tròn Giải giúp mình với
KT
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A, widehat{BAC}120^o, ABACa. Tam giác SAB vuông tại B, tam giác SAC vuông tại C, góc giữa hai mặt phẳng left(SABright) và left(ABCright) bằng 60^o. Gọi H là hình chiếu vuông góc của điểm S lên mặt phẳng left(ABCright). Chứng minh rằng HB vuông góc AB và tính thể tích khối chóp S.ABC theo a
Đọc tiếp
Cho hình chóp \(S.ABC\) có đáy \(ABC\) là tam giác vuông cân tại \(A\), \(\widehat{BAC}=120^o\), \(AB=AC=a\). Tam giác \(SAB\) vuông tại \(B\), tam giác \(SAC\) vuông tại \(C\), góc giữa hai mặt phẳng \(\left(SAB\right)\) và \(\left(ABC\right)\) bằng \(60^o\). Gọi \(H\) là hình chiếu vuông góc của điểm \(S\) lên mặt phẳng \(\left(ABC\right)\). Chứng minh rằng \(HB\) vuông góc \(AB\) và tính thể tích khối chóp \(S.ABC\) theo \(a\)
Cho tam giác ABC. Vẽ điểm O cách đều ba đỉnh A, B, C trong mỗi trường hợp sau:
a) Tam giác ABC nhọn;
b) Tam giác ABC vuông tại A;
c) Tam giác ABC có góc A tù.
a) Tam giác ABC nhọn:
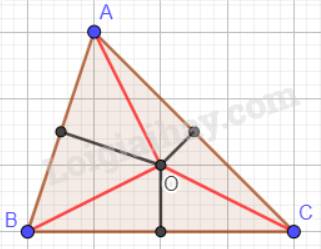
b) Tam giác ABC vuông tại A:
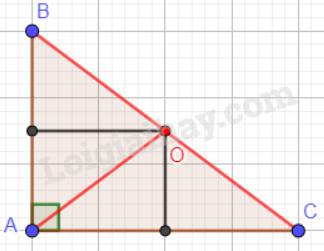
c) Tam giác ABC có góc A tù:
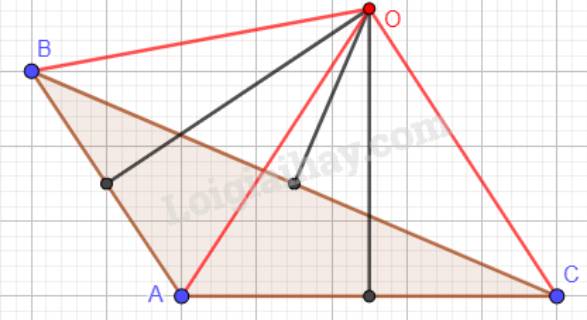
Đúng 0
Bình luận (0)
Cho hình vẽ, biết tam giác OAB vuông tại A, CDFE là hình vuông có diện tích bằng 24, tam giác ODC vuông cân tại O và diện tích của tam giác BDG bằng 32. Tính diện tích tam giác ABC.
Đọc tiếp
Cho hình vẽ, biết tam giác OAB vuông tại A, CDFE là hình vuông có diện tích bằng 24, tam giác ODC vuông cân tại O và diện tích của tam giác BDG bằng 32. Tính diện tích tam giác ABC.
Bai 10: Cho tam giác ABC vuông cân tại A . Vẽ tamgiác OBC vuông tại O sao cho O va A thuộc hai nửamặt phẳng đối nhau bờ BC. Chứng minh rằng tia OAlà tia phân giác của góc BOC.Bai 11: Cho tam giac ABC vuông cân tại A. Gọi M làtrung điểm của BC. Lấy điểm N nằm giữa M và C.Vẽ BH vuông góc AN . Chứng minh rằng khi diểm N di độngthi tia phân giác của góc BHN luôn đi qua một điểm cốđịnh.Jup mik vs mn ưi))
Đọc tiếp
Bai 10: Cho tam giác ABC vuông cân tại A . Vẽ tam
giác OBC vuông tại O sao cho O va A thuộc hai nửa
mặt phẳng đối nhau bờ BC. Chứng minh rằng tia OA
là tia phân giác của góc BOC.
Bai 11: Cho tam giac ABC vuông cân tại A. Gọi M là
trung điểm của BC. Lấy điểm N nằm giữa M và C.
Vẽ BH vuông góc AN . Chứng minh rằng khi diểm N di động
thi tia phân giác của góc BHN luôn đi qua một điểm cố
định.
Jup mik vs mn ưi=))
Cho tam giác ABC . Vẽ ra phía ngoài của tam giác này các tam giác vuông cân tại A là tam giác ABE và ACF . Vẽ AH vuông góc BC tại H . Đường thẳng AH cắt EF tại O ,kẻ EI vuông góc CH tại I
a)CMR : EI = AH
b) Cm O là trung điểm EF
Bạn tham khảo ở đây nhé
Câu hỏi của be hat tieu - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Tam giác ABC vuông tại A, AB=3, AC=4. phân giác góc C cắt phân giác góc B tại O, vẽ OE vuông AB, OF vuông AC
a) cm AB+AC-BC=2AE
b) O tới các cạnh tam giác
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.Bài 2: Cho tam giác ABC có góc A 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM...
Đọc tiếp
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.
Bài 2: Cho tam giác ABC có góc A= 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.
Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM vuông góc với CN.
Mọi người giúp mình nhanh nha😙😙😙😙
Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC . Từ A dựng ra ngoài 2 tam giác vuông cân tại A ,đó là tam giác EAB và tam giác FAC . đường cao AH kéo dài gặp EF tại O . chứng minh OE = OF
Xét tam giác ABC cân tại A có đường cao AH
=> AH là đường phân giác
=> \(\widehat{BAH}=\widehat{CAH}\)(1)
Ta có: \(\widehat{EAB}=\widehat{FAC}=90^o\)(2)
Mặt khác: \(\widehat{OAH}=\widehat{OAE}+\widehat{EAB}+\widehat{BAH}=\widehat{OAF}+\widehat{FAC}+\widehat{CAH}\)(3)
Từ (1), (2), (3) => \(\widehat{OAE}=\widehat{OAF}\)
Ta lại có Tam giác EAB cân tại A, BAC cân tại A, CAF cân tại A
=> AE=AB=AC=AF
Xét tam giác EOA và tam giác FOA có:
AF=AE
\(\widehat{OAE}=\widehat{OAF}\)
OA chung
=> \(\Delta EOA=\Delta FOA\)
=> OE=OF
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AC=6cm, góc B =30o
a) Giải tam giác vuông ABC
b) Vẽ đường cao Ah và trung tuyến Am của tam giác ABC. Tính diện tích tam giá AHM
Cho tam giác ABC vuông tại A có góc B= 50 độ nội tiếp (O,4cm) . Vẽ dây AD vuông AB tại I
a) C/m ba điểm B , I , C thẳng hàng
b) Giải tam giác vuông ABC
c) C/m IB.IC=IA.ID
a: Sửa đề: vẽ dây AD vuông góc với đường kính của (O) tại I
ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
=>BC là đường kính của (O)
mà AD vuông góc với đường kính của (O)
nên AD\(\perp\)BC tại I
=>B,I,C thẳng hàng
b: BC=2*OB=8cm
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-50^0=40^0\)
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{8}=sin40\)
=>\(AB\simeq5,14\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{8^2-5.14^2}\simeq6,13\left(cm\right)\)
c: ΔOAD cân tại O
mà OI là đường cao
nên I là trung điểm của AD
ΔABC vuông tại A có AI là đường cao
nên \(AI^2=IB\cdot IC\)
=>\(IB\cdot IC=IA\cdot ID\)
Đúng 0
Bình luận (0)





