tìm các số a,b,c sao cho 2a=3b;5b=7c và 3a + 5c -7b = 30
PH
Những câu hỏi liên quan
Tìm các số nguyên tố a,b,c sao cho 2a+3b+6c =78
Xem thêm câu trả lời
Tìm các số nguyên tố a,b,c sao cho:2a+3b+6c=78
Ta có :
2a và 6v là số chẵn mà 78 là số chẵn
=> 3b phải là số chẵn = > b là số chẵn mà b là số nguyên tố
b = 2 ( 2 là số nguyên tố chẵn duy nhất )
Ta có : 2a + 6 + 6c = 78
=> 2a + 6c = 72
=> a + 3c = 36 ( chia 2 vế cho 2 )
Ta có 36 chia hết cho 3 thì 3c chia hết cho 3
=> a phải chia hết cho 3 . Mà a là số nguyên tố
=> a = 3 ( số nguyên tố duy nhất chia hết cho 3 )
=> 3+ 3c = 36 => c = 11
= > a = 3 , b = 2 , c = 11
Chúc bạn học tốt :))
Tìm các số a, b, c sao cho:
2a = 3b, 5b = 7c và 3a + 5c – 7b = 30
Tìm các số nguyên tố a,b,c sao cho 2a + 3b + 6c = 78
tìm số nguyên tố a,b,c sao cho 2a+3b+6c=78 đây bn nhé
Đúng 0
Bình luận (0)
Tìm các số nguyên tố a, b, c sao cho 2a + 3b + 6c= 78
Vì 78 chia hết cho 2 mà 2a;6c chia hết cho 2\(\Rightarrow\)3b chia hết cho 2 mà b là số nguyên tố\(\Rightarrow\)b=2
Thay b = 2 ta có:
2a+3*2 + 6c=78
2a+6+6c=78
2a+6c=78-6
2a+6c=72
Vì 72 chia hết cho 3 mà 6c chia hết cho 3\(\Rightarrow\)2a chia hết cho 3 mà a là số nguyên tố\(\Rightarrow\)a=3
Thay a=3 ta có:
2*3 + 6c=72
6+6c=72
6c=72-6
6c=66
c=66/6
c=11
Vậy a=3;b=2;c=11
Đúng 0
Bình luận (0)
Tìm các số nguyên a, b sao cho: ab+11=2a+3b
Lời giải:
$ab+11=2a+3b$
$ab-2a-3b+11=0$
$a(b-2)-3(b-2)+5=0$
$(a-3)(b-2)=-5$
Vì $a,b$ là số nguyên nên $a-3, b-2$ là số nguyên. Ta có bảng sau: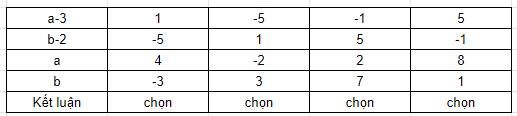
Đúng 1
Bình luận (0)
Tìm các số nguyên a, b sao cho: ab + 11 = 2a + 3b
Tìm số nguyên tố a, b, c sao cho:2a + 3b +6c=78
Xem chi tiết
\(2a+3b+6c=78\)
có \(2a,6c,78\)là số chẵn nên \(3b\)là số chẵn, suy ra \(b=2\).
\(\Rightarrow2a+6c=72\Leftrightarrow a+3c=36\)
có \(3c⋮3,36⋮3\)suy ra \(a⋮3\Rightarrow a=3\).
\(\Rightarrow c=\frac{36-3}{3}=11\)(thỏa mãn)
Vậy \(\left(a,b,c\right)=\left(3,2,11\right)\)
Tìm các số a , b ,c sao cho :
2a = 3b, 5b = 7c và 3a +5c - 7b = 30
Khó quá jup #Rau vs
Ta có :
\(\begin{cases}2a=3b\\5b=7c\end{cases}\)
\(\Rightarrow\begin{cases}\frac{a}{3}=\frac{b}{2}\\\frac{b}{7}=\frac{c}{5}\end{cases}\)
\(\Rightarrow\begin{cases}\frac{a}{21}=\frac{b}{14}\\\frac{b}{14}=\frac{c}{10}\end{cases}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
\(\Rightarrow\frac{3a}{62}=\frac{7b}{98}=\frac{5c}{50}\)
Áp dụng tc của dãy tỉ số bằng nhau ta có :
\(\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}=\frac{3a+5c-7b}{63-50+98}=\frac{30}{111}=\frac{10}{37}\)
Giải ra tìm được a ; b ; c
Đúng 0
Bình luận (0)
