Xét ba số thực a;b;c thay đổi thuộc đoạn [0;3]. Giá trị lớn nhất của biểu thức T = 4 ( a - b ) ( b - c ) ( c - a ) ( a b + b c + c a ) - ( a 2 + b 2 + c 2 ) là
PB
Những câu hỏi liên quan
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sauTrong ba mệnh đề (I),(II),(III), số mệnh đề sai là A. 2 B. 0 C. 3 D. 1
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
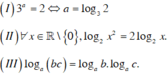
Trong ba mệnh đề (I),(II),(III), số mệnh đề sai là
A. 2
B. 0
C. 3
D. 1
Cho a, b, c là ba số thực thỏa mãn điều kiện
a
3
36 và abc 1 Xét tam thức bậc haiTừ câu a) suy ra
Đọc tiếp
Cho a, b, c là ba số thực thỏa mãn điều kiện a 3 > 36 và abc = 1
Xét tam thức bậc hai
Từ câu a) suy ra
Cho a, b, c là ba số thực thỏa mãn điều kiện a 3 > 36 và abc = 1
Xét tam thức bậc hai
Chứng minh rằng f(x) > 0, ∀x
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
I
3
a
2
⇔
a
log
3
2
I
I
∀
x
∈
ℝ
0
,
log
2
x
2...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
I 3 a = 2 ⇔ a = log 3 2 I I ∀ x ∈ ℝ \ 0 , log 2 x 2 = 2 log 2 x I I I log a b c = log a b . log a c
Trong ba mệnh đề I , I I , I I I số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a,b,c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau
(
I
)
3
a
2
⇔
a
log
3
2
(
II
)
∀
x
∈
R
{
0
}
,
log
2
x
2
2
log...
Đọc tiếp
Cho a,b,c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau
( I ) 3 a = 2 ⇔ a = log 3 2
( II ) ∀ x ∈ R \ { 0 } , log 2 x 2 = 2 log 2 x
( III ) log a ( bc ) = log a b . log a c
Trong ba mệnh đề (I), (II), (III) số mệnh đề sai là
A. 2
B. 3
C. 1
D. 0
Cho a, b, c là các số thực dương,
a
≠
1
. Xét các mệnh đề sau:(I)
2
a
3
⇔
a
log
2
3
(II)
∀
x
∈
ℝ
0
,
log
3
x
2
2
log
3
x
(III) ...
Đọc tiếp
Cho a, b, c là các số thực dương, a ≠ 1 . Xét các mệnh đề sau:
(I) 2 a = 3 ⇔ a = log 2 3
(II) ∀ x ∈ ℝ \ 0 , log 3 x 2 = 2 log 3 x
(III) log a b . c = log a b . log a c
Trong ba mệnh đề (I), (II), (III), tổng số mệnh đề đúng là?
A. 3
B. 2
C. 1
D. 0
Đáp án C
Mệnh đề (I) đúng.
Mệnh đề (II) sai vì log 3 x 2 = 2 log 3 x khi x > 0 nên điều kiện ∀ x ∈ ℝ \ 0 là chưa đủ.
Mệnh đề (III) sai vì log a b . c = log a b + log a c
Số mệnh đề đúng là 1.
Đúng 0
Bình luận (0)
H24
SGK Cánh diều - Tập 2 - Trang 63
29 tháng 10 2023 lúc 23:35
a) Tính rồi so sánh:
Nhận xét: Khi nhân một tích hai phân số với phân số thứ ba, ta có thể nhân phân số thứ nhất với tích của phân số thứ hai và phân số thứ ba.
b) Lấy ví dụ tương tự câu a rồi đố bạn thực hiện.
$\left( {\frac{1}{4} \times \frac{2}{3}} \right) \times \frac{3}{5} = \frac{1}{6} \times \frac{3}{5} = \frac{1}{{10}}$
$\frac{1}{4} \times \left( {\frac{2}{3} \times \frac{3}{5}} \right) = \frac{1}{4} \times \frac{2}{5} = \frac{1}{{10}}$
Vậy $\left( {\frac{1}{4} \times \frac{2}{3}} \right) \times \frac{3}{5}$ = $\frac{1}{4} \times \left( {\frac{2}{3} \times \frac{3}{5}} \right)$
$\left( {\frac{1}{2} \times \frac{1}{6}} \right) \times \frac{1}{5} = \frac{1}{{12}} \times \frac{1}{5} = \frac{1}{{60}}$
$\frac{1}{2} \times \left( {\frac{1}{5} \times \frac{1}{6}} \right) = \frac{1}{2} \times \frac{1}{{30}} = \frac{1}{{60}}$
Vậy $\left( {\frac{1}{2} \times \frac{1}{6}} \right) \times \frac{1}{5}$ = $\frac{1}{2} \times \left( {\frac{1}{5} \times \frac{1}{6}} \right)$
b) Ví dụ: $\left( {\frac{2}{5} \times \frac{1}{3}} \right) \times \frac{3}{7}$ = $\frac{2}{5} \times \left( {\frac{1}{3} \times \frac{3}{7}} \right)$
Đúng 0
Bình luận (0)
H24
27 tháng 4 2022 lúc 13:35
xét ba số thực a,b,c thỏa mãn 0 ≤ a,b,c ≤ 2 và a+b+c = 3. Tìm giá trị nhỏ nhất của biểu thức : P = a3+ b3+ c3 + \(\dfrac{\left(ab+bc+ca\right)^3+8}{ab+bc+ca}\)
1 loài thực vật có bộ NST 2n = 10. Trên mỗi cặp NST số 1 và số 2 xét 1 gen có 1 alen, trên mỗi cặp NST số 3, số4 và số 5 xét 1 gen có 2 alen. Do đột biến, trong loài đã xuất hiện 5 dạng thể ba tương ứng với các cặp NST. Theo lí thuyết, các thể ba này có tối đa bao nhiêu kiểu gen về các gen đang xét
- Xét cặp 1, 2
+ 2 loại KG đột biến là AAA, aaa
+ KG bình thường có 2 loại: A, a
- Xét cặp 3,4,5
+ 4 loại KG đột biến: AAA, AAa. Aaa. aaa
+ 3 loại KG bt: AA, Aa, aa
Các dạng thể ba có tối đa số KG là: (4 x 32 x 2 x 3) + (2 x 21 x 33 x 2) = 432
Đúng 1
Bình luận (0)