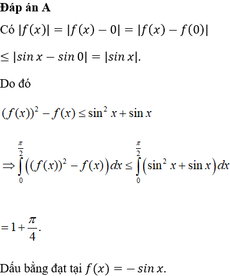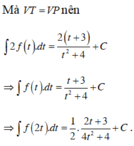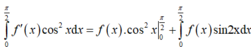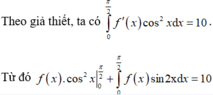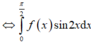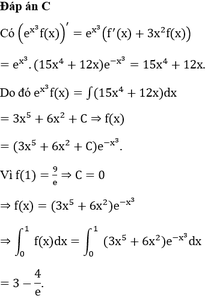Cho hàm số y = f(x) thoả mãn trên R , f(1)=1 và nguyên hàm tích phân từ [0;1] bằng 1/3 . Tính I= nguyên hầm tích phân từ [0-pi/2] của sin2x.f’(sinx)dx
KD
Những câu hỏi liên quan
Cho hàm số f(x) liên tục trên R thoả mãn f(0)0 và
|
f
(
x
)
-
f
(
y
)
|
≤
|
sin
x
-
sin
y
|
với mọi
x
,
y
∈
R
. Giá trị lớn nhất của tích phân
∫
0
π
2
(
(
f
(
x...
Đọc tiếp
Cho hàm số f(x) liên tục trên R thoả mãn f(0)=0 và | f ( x ) - f ( y ) | ≤ | sin x - sin y | với mọi x , y ∈ R . Giá trị lớn nhất của tích phân ∫ 0 π 2 ( ( f ( x ) ) 2 - f ( x ) ) d x bằng
A. π 4 +1
B. π 8
C. 3 π 8
D. 1- π 4
Cho hàm số f(x) liên tục trên R+ và thoả mãn
∫
f
(
x
+
1
)
x
+
1
d
x
2
(
x
+
1
+
3...
Đọc tiếp
Cho hàm số f(x) liên tục trên R+ và thoả mãn ∫ f ( x + 1 ) x + 1 d x = 2 ( x + 1 + 3 ) x + 5 + C . Nguyên hàm của hàm số f(2x) trên tập R+ là
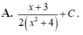
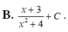
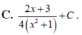
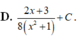
Cho hàm số f(x) xác định và liên tục trên R và có đạo hàm f'(x) thoả mãn f'(x) = (1 - x)(x+2)g(x) + 2023 với g(x) < 0, ∀x∈R. Hàm số y = f(1-x) + 2023x + 2024 nghịch biến trên khoảng nào?
Cho hàm số
y
f
(
x
)
có đạo hàm trên R thỏa mãn
3
f
x
.
e
f
3
x
-
x
2
-
1
-
2
x...
Đọc tiếp
Cho hàm số y = f ( x ) có đạo hàm trên R thỏa mãn 3 f ' x . e f 3 x - x 2 - 1 - 2 x f 2 x = 0 và f ( 0 ) = 1 . Tích phân ∫ 0 7 x . f x d x bằng
A. 2 7 3
B. 15 4
C. 45 8
D. 5 7 4
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn
[
f
(
x
)
]
2
+
f
(
x
)
f
(
x
)
≥
1
,
∀
x
∈
[
0
;
1
]
và
f
2
(
0
)
+
f
(...
Đọc tiếp
Cho hàm số f (x) có đạo hàm cấp hai liên tục trên đoạn [0;1] thoả mãn [ f ' ( x ) ] 2 + f ( x ) f '' ( x ) ≥ 1 , ∀ x ∈ [ 0 ; 1 ] và f 2 ( 0 ) + f ( 0 ) . f ' ( 0 ) = 3 2 . Giá trị nhỏ nhất của tích phân ∫ 0 1 f 2 ( x ) d x bằng
A. 5 2
B. 1 2
C. 11 6
D. 7 2
Cho hàm số y f (x) thoả mãn
f
(
x
)
+
2
f
(
1
-
x
)
(
2
x
+
1
)
e
x
,
∀
x
∈
R
Tích phân
∫
0
1
3
f
(
3
x
)
d
x...
Đọc tiếp
Cho hàm số y = f (x) thoả mãn f ( x ) + 2 f ( 1 - x ) = ( 2 x + 1 ) e x , ∀ x ∈ R Tích phân ∫ 0 1 3 f ( 3 x ) d x bằng
A. e + 1 3
B. e + 1
C. e + 1 9
D. 3 e + 1
Đặt ![]()
![]()
Khi đó
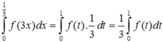
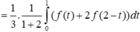
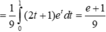
Chọn đáp án C. *Chú ý tính chất tích phân:
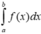
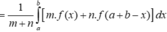
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hàm số f(x) có đạo hàm và liên tục trên
0
;
π
2
, thoả mãn
∫
0
π
/
2
f
x
cos
2...
Đọc tiếp
Cho hàm số f(x) có đạo hàm và liên tục trên 0 ; π 2 , thoả mãn ∫ 0 π / 2 f ' x cos 2 x d x = 10 và f(0)= 3. Tích phân ∫ 0 π / 2 f x sin 2 x d x bằng
A. -13
B. 13
C. 7
D. -7
Cho hàm số
y
f
(
x
)
liên tục trên R và có hàm số
y
f
(
x
)
thoả mãn. Số cực trị của hàm số
y
f
(
x
)
là A. 3 B. 1 C. 0 D. 2
Đọc tiếp
Cho hàm số y = f ( x ) liên tục trên R và có hàm số y = f ' ( x ) thoả mãn. Số cực trị của hàm số y = f ( x ) là
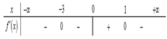
A. 3
B. 1
C. 0
D. 2
Cho hàm số yf(x) có đạo hàm liên tục trên R thỏa mãn
x
f
x
.
f
x
f
2
x
-
x
,
∀
x
∈
R
và f(2)1 Tích phân
∫
0
2
f
2
x
d
x
bằng A.
3...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn x f x . f ' x = f 2 x - x , ∀ x ∈ R và f(2)=1 Tích phân ∫ 0 2 f 2 x d x bằng
A. 3 2
B. 4 3
C. 2
D. 4
Cho hàm số f(x) thoả mãn
f
(
1
)
9
e
và
f
(
x
)
+
3
x
2
f
(
x
)
(
15
x
4
+
12
x
)
e
-
x...
Đọc tiếp
Cho hàm số f(x) thoả mãn f ( 1 ) = 9 e và f ' ( x ) + 3 x 2 f ( x ) = ( 15 x 4 + 12 x ) e - x 3 , ∀ x ∈ R . Tích phân ∫ 0 1 f ( x ) d x bằng
A. 3 + 4 e
B. 2e - 1
C. 3 - 4 e
D. 2e + 1