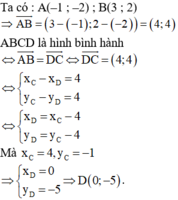cho hình bình hành ABCD có đỉnh A(2;4). Biết 2 điểm M(-1;3) và N(5;1) lần lượt thuộc 2 cạnh AD, BC sao cho AM=CN. tìm tọa độ trọng tâm tam giác BCD
TT
Những câu hỏi liên quan
cho hình bình hành ABCD có 4 đỉnh lần lượt nằm trên hình bình hành MNPQ. CM:2 hình bình hành này có cùng tâm đối xứng
Cho hình bình hành EFGH có 4 đỉnh lần lượt nằm trên 4 cạnh của hình bình hành ABCD. Chứn minh rằng 2 hình bình hành này có cùng 1 tâm đối xứng
Cho hình bình hành ABCD có A(-3;-1) B(2;2) giao điểm 2 đường chéo thuộc đường
thẳng x-6y-3=0 diện tích hình bình hành bằng 26. Tìm tọa độ các đỉnh.
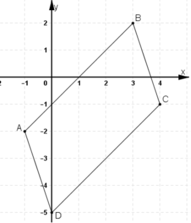
Cho hình bình hành ABCD có A(-1; -2), B(3;2), C(4; -1). Tìm tọa độ của đỉnh D.
Cho hình bình hành ABCD có diện tích là 36cm2. Tính chu vi của hình bình hành đó biết chiều cao hạ từ đỉnh A vuông góc với cạnh DC là 3cm và bằng 
1/2 chiều cao hạ từ đỉnh D vuông góc với cạnh AD?
Cho hình bình hành ABCD có H, K lần lượt là các chân đường cao kẻ từ đỉnh A,C xuống BD. Chứng minh AHCK là hình bình hành
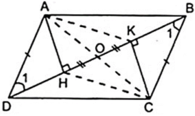
Từ giả thiết ta có:
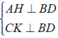
⇒ AH//CK. ( 1 )
Áp dụng tính chất về cạnh của hình bình hành và tính chất của các góc so le ta có:
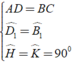
⇒ Δ ADH = Δ CBK
(trường hợp cạnh huyền – góc nhọn)
⇒ AH = CK (cạnh tương tứng bằng nhau) ( 2 )
Từ ( 1 ) và ( 2 ) ta có tứ giác AHCK có cặp cạnh đối song song và bằng nhau là hình bình hành.
Đúng 1
Bình luận (0)
Cho hình hộp đứng
A
B
C
D
.
A
B
C
D
.
Xét tất cả các hình bình hành có đỉnh là đỉnh của hình hộp đó. Hỏi có bao nhiêu hình bình hành mà mặt phẳng chứa nó vuông góc với mặt phẳng đáy (ABCD)? A. 4 B. 6 C. 8 D. 10
Đọc tiếp
Cho hình hộp đứng A B C D . A ' B ' C ' D ' . Xét tất cả các hình bình hành có đỉnh là đỉnh của hình hộp đó. Hỏi có bao nhiêu hình bình hành mà mặt phẳng chứa nó vuông góc với mặt phẳng đáy (ABCD)?
A. 4
B. 6
C. 8
D. 10
Đáp án B
Cách giải:
Có 6 hình bình hành thỏa mãn yêu cầu:
A B B ' A ' ; B C C ' B ' ; C DD ' C ' ; A D D ' A ' ; A C C ' A ' ; B DD ' B '
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD có chiều dài cạnh CD = 8cn , cạnh bên AD = 6 cm và chiều cao nối từ đỉnh A xuống cạnh CD dài 5cm. Tính chu vi, diện tích của hình bình hành ABCD?
Cho hình bình hành ABCD có tọa độ ba đỉnh là : A(3 ; -2) , B(14 ; -2) , D(0 ; -8) . Tính tọa độ C (... ; ...) ?
Cho hình bình hành ABCD. Các tia phân giác của các góc của hình bình hành cắt nhau tạo thành tứ giác EFGH.
a) Tứ giác EFGH là hình gì ? Vì sao ?
b) Chứng minh rằng EG = FH và bằng hiệu giữa hai cạnh kề một đỉnh của hình bình hành ABCD.
c) Hình bình hành ABCD cần có thêm điều kiện gì để EFGH là hình vuông?