Cho tâm I(2;1),(d):2x+3y+4=0. Viết phương trình (d') qua phép quay tâm I góc quay 40\(^0\)
VT
Những câu hỏi liên quan
Cho đường tròn tâm O, bán kính R, đường kính AB, vẽ đường tròn tâm I, đường kính OA. a. Chm 2 đường tròn tâm O và tâm I tiếp xúc nhau, b. Dây AC của đường tròn tâm O cắt tâm I tại D. Chm ID//OC. c. Biết AC = R căn 3 . Tính theo R , diện tích ODCB
a:
I nằm giữa O và A
=>OI+IA=OA
=>OI=OA-AI
=R-R'
=>(O) với (I) tiếp xúc nhau tại A
b: ΔIAD cân tại I
=>góc IAD=góc IDA
=>góc IDA=góc OAC
ΔOAC cân tại O
=>góc OAC=góc OCA
=>góc IDA=góc OCA
mà hai góc này đồng vị
nên ID//OC
c: Xét (I) có
ΔADO nội tiếp
AO là đường kính
=>ΔADO vuông tại D
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó; ΔACB vuông tại C
Xét ΔACB vuông tại C có cos CAB=AC/AB=1/2*căn 3
=>góc CAB=30 độ
CB=căn AB^2-AC^2=R/2
\(S_{CAB}=\dfrac{1}{2}\cdot CA\cdot CB=\dfrac{1}{2}\cdot\dfrac{R\sqrt{3}}{2}\cdot\dfrac{1}{2}R=\dfrac{R^2\sqrt{3}}{8}\)
Xét ΔADO vuông tại D và ΔACB vuông tại C có
góc DAO chung
Do đó: ΔADO đồng dạng với ΔACB
=>\(\dfrac{S_{ADO}}{S_{ACB}}=\left(\dfrac{AO}{AB}\right)^2=\left(\dfrac{1}{4}\right)\)
=>\(S_{ODCB}=\dfrac{3}{4}\cdot S_{ACB}=\dfrac{3}{4}\cdot\dfrac{R^2\sqrt{3}}{8}=\dfrac{3\cdot\sqrt{3}\cdot R^2}{32}\)
Đúng 0
Bình luận (0)
Cho 2 đường tròn tâm I và tâm K có cùng bán kính 1,5 cm cắt nhau tại A và B. Vẽ dây cung AC của đường tron tâm I sao cho AC=AB. Chứng minh góc IAC=IAB=KAB
Cho 2 đường tròn tâm I và tâm K có cùng bán kính 1,5 cm. chúng cắt nhau tại A và B. vẽ dây cung AC của đường tròn tâm I sao AC = Ab. chứng minh IAC = IAB = KAB
Cho đường tròn tâm O và dây AB cố định, điểm M tùy ý thay đổi trên đoạn AB. Qua A và M dựng đường tròn tâm I tiếp xúc đường tròn tâm O tại A. Qua B và M dựng đường tròn tâm J tiếp xúc đường tròn tâm O tại B. 2 đường tròn tâm I và đường tròn tâm J cắt nhau tại điểm thứ 2 là N. CMR MN luôn đi qua 1 điểm cố định
Cho mệnh đề:1) Mặt cầu có tâm I(3;-2;4) và đi qua A(7;2;1) là
(
x
-
3
)
2
+
(
y
+
2
)
2
+
(
z
-
4
)
2
41
2) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oxy) là
(
x
-
2
)
2
+...
Đọc tiếp
Cho mệnh đề:
1) Mặt cầu có tâm I(3;-2;4) và đi qua A(7;2;1) là ( x - 3 ) 2 + ( y + 2 ) 2 + ( z - 4 ) 2 = 41
2) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oxy) là ( x - 2 ) 2 + ( y - 1 ) 2 + ( z + 3 ) 2 = 9
3) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oxz) là ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 1
4) Mặt cầu có tâm I(2;-1;3) và tiếp xúc với mp (Oyz) là ( x - 2 ) 2 + ( y + 1 ) 2 + ( z - 3 ) 2 = 4
Số mệnh đề đúng là bao nhiêu:
A. 4
B. 1
C. 2
D. 3
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số
1
2
. A.
x
-
4
2
+
(
y
+
4
)
2
4
B. ...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy cho đường tròn tâm I(2;-2), bán kính R = 4. Viết phương trình đường tròn là ảnh của đường tròn (I;R) qua phép vị tự tâm O, tỉ số 1 2 .
A. x - 4 2 + ( y + 4 ) 2 = 4
B. x - 4 2 + ( y + 4 ) 2 = 64
C. x - 1 2 + ( y + 1 ) 2 = 4
D. x - 1 2 + ( y + 1 ) 2 = 64
Trong mặt phẳng Oxy cho điểm I(1;1) và đường tròn tâm I bán kính 2. Viết phương trình đường tròn là ảnh của đường tròn trên qua phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc 45 o và phép vị tự tâm O, tỉ số căn 2 .
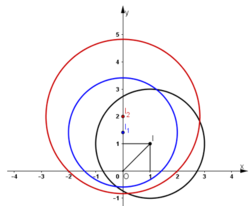
+ Gọi (I1; R1) = Q(O; 45º) (I; R) (Phép quay đường tròn tâm I, bán kính R qua tâm O một góc 45º).
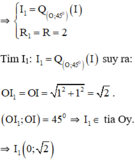
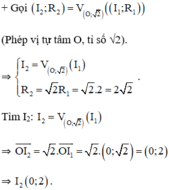
Vậy phương trình đường tròn cần tìm là (I2; R2): x2 + (y – 2)2 = 8.
Đúng 0
Bình luận (0)
Cho 2 đường tròn tâm O và tâm O cắt nhau tại A và B. 2 tâm đường tròn nằm trên 2 mặt phẳng bờ AB Qua B kẻ cát tuyến vuông góc với AB cắt đường tròn tâm O ở C và cắt đường tròn tâm O ở D. Tia Ca cắt đường tròn tâm O ở I. Tia DA cắt đường tròn tâm O tại K.Chứng minh tứ giác CKID là tứ giác nội tiếpGọi M là giao điểm của CK và DI. chứng minh M, A, B thẳng hàng
Đọc tiếp
Cho 2 đường tròn tâm O và tâm O' cắt nhau tại A và B. 2 tâm đường tròn nằm trên 2 mặt phẳng bờ AB Qua B kẻ cát tuyến vuông góc với AB cắt đường tròn tâm O ở C và cắt đường tròn tâm O' ở D. Tia Ca cắt đường tròn tâm O' ở I. Tia DA cắt đường tròn tâm O tại K.
Chứng minh tứ giác CKID là tứ giác nội tiếp
Gọi M là giao điểm của CK và DI. chứng minh M, A, B thẳng hàng
Cho 2 đường tròn tâm I vs K có bán kính 1,5cm , chúng cắt nhau tại A và B. Vẽ dây AC của đường tròn tâm I sao cho AC=AC=B. Chứng minh rằng IAC=IAB=KAB
+) Ta có:
AC=AB=>^AC=^AB
^ACD=^ABD
^CD=^BP=>^CDA=^BAD hay ^IAC=IAB(1)
+) Ta có:
Đường tròn I=Đường tròn K (Vì chung R=1,5 cm)
Cung AB của đường tròn K
=>DB=DE
=>^IAB=^KAB(2)
Từ (1) và (2) suy ra:
^IAC=^IAB=^KAB
Đúng 0
Bình luận (0)
Cho 2 đường tròn tâm I vs K có bán kính 1,5cm , chúng cắt nhau tại A và B. Vẽ dây AC của đường tròn tâm I sao cho AC=AC=B. Chứng minh rằng IAC=IAB=KAB