Cho đường thẳng (d): Ax + By = C(A2 + B2 ≠ 0). Tính khoảng cách từ gốc tọa độ O (0;0) đến đường thẳng (d) trong 3 trường hợp:
1) A≠0, B=0
2) A = 0, B≠0
3) AB ≠ 0
công thức tinh khoảng cách từ gốc tọa độ 0 đến đường thẳng ax+by+c=0 là gì?
Đồ thị hàm số hả bạn?
Mình đoán thế
Có đúng ko?
O(0;0) thê vao pt ax+by+c=0 rôi lây tri tuyêt đôi ,sau đo đem chia cho \(\sqrt{a^2+b^2}\) ta đc khoang cach tu O đên đuong thang cân tim đên (d)=/c/\(\sqrt{\left(a^2+b^2\right)}\)
cho đường thẳng (d):y=2x+17 và (đ):y=-x-5. Gọi A và B là hai điểm lần lượt trên (d) và (đ) và đối xứng qua Ox. Tọa độ của A và B là gì?
Bài 5: Cho (d): y = -2x + 3
a) Tìm tọa độ giao điểm A, B của ĐTHS lần lượt với Ox, Oy
b) Tính khoảng cách từ gốc tọa độ đến đường thẳng (d)
c) Tính khoảng cách từ C(0; -2) đến đường thẳng (d)
\(a,\) Pt hoành độ giao điểm
\(x=0\\ \Leftrightarrow y=-2\cdot0+3=3\\ \Leftrightarrow A\left(0;3\right)\)
Pt tung độ giao điểm
\(y=0\\ \Leftrightarrow0=-2x+3\Leftrightarrow x=\dfrac{3}{2}\\ \Leftrightarrow B\left(\dfrac{3}{2};0\right)\)
Cho đường thẳng (d) : y=ax+3 ( a khác 0). Cho biết khoảng cách từ gốc tọa độ đến (d) là (3căn2)/2 . Xác định a.
Trong không gian với hệ tọa độ Oxyz, mặt phẳng ( P ) : a x + b y + c z + d = 0 , a 2 + b 2 + c 2 > 0 đi qua điểm B(1;0;2) , C(-1;-1;0) và cách A(2;5;3) một khoảng lớn nhất. Khi đó giá trị của biểu thức M = a + c b + d là
A. M = 1
B. M = 3 4
C. M = - 2 7
D. M = - 3 2
Đáp án C.
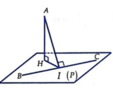
Ta có B C → = - 2 ; - 1 ; - 2 nên phương trình đường thẳng BC là x = 1 - 2 t y = - t ( t ∈ ℝ ) z = 2 - 2 t .
Gọi I là hình chiếu vuông góc của A trên BC, H là hình chiếu vuông góc của A trên mặt phẳng (P) . Khi đó A H = d A ; P ≤ A I và AH đạt giá trị lớn nhất khi H ≡ I . Suy ra mặt phẳng (P) qua I và vuông góc với AI.
Từ I ∈ B C ⇒ I 1 - 2 t ; - t ; 2 - 2 t và A I → = - 1 - 2 t ; - t - 5 ; - 1 - 2 t .
Lại có A I ⊥ B C ⇔ A I → . B C → = 0 ⇔ 2 ( 1 + 2 t ) + ( t + 5 ) + 2 ( 1 + 2 t ) = 0 ⇔ t = - 1 .
Mặt phẳng (P) đi qua I(3;1;4) và nhận VTPT là A I → = 1 ; - 4 ; 1 nên có phương trình tổng quát là: x - 4 y + z - 3 = 0 .
Vậy a = 1 , b = - 4 , c = 1 , d = - 3 → M = 1 + 1 - 4 - 3 = - 2 7 .
Cho \(_{\Delta ABC}\) cân B, đỉnh A(1;-1), C(3;5). Đỉnh B thuộc d:2x-y=0. Viết pt đường thẳng AB, BC. Tính khoảng cách từ gốc tọa độ đến đường thẳng BC.
cho đường thẳng (d): y=m(2x-1)+3-2x
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) bằng 1.
a) Tìm m để khoảng cách từ gốc tọa độ O đến đường thẳng (d) đạt giá trị lớn nhất.
Trong mặt phẳng Oxy , đường thẳng d : a x + b y + c = 0 , a 2 + b 2 ≠ 0 . Vectơ nào sau đây là một vectơ pháp tuyến của đường thẳng d ?
A. n → = a ; - b
B. n → = b ; a
C. n → = b ; - a
D. n → = a ; b
Chọn D.
Ta có một vecto pháp tuyến của đường thẳng d là n → = a ; b
Cho đường thẳng d : y = (m + 2)x +2m - 6 ( m ≠ 2). Tính khoảng cách từ gốc tọa độ O cho đến đường thẳng d biết A(2;6) ∈ d
Thay x=2 và y=6 vào (d), ta được:
2(m+2)+2m-6=6
=>4m+4+2m-6=6
=>6m-2=6
=>6m=8
=>\(m=\dfrac{4}{3}\)
Khi m=4/3 thì (d): \(y=\left(\dfrac{4}{3}+2\right)x+2\cdot\dfrac{4}{3}-6=\dfrac{10}{3}x-\dfrac{10}{3}\)
Gọi A(x,y) và B(x,y) lần lượt là giao điểm của (d) với trục Ox và Oy
Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\\dfrac{10}{3}x-\dfrac{10}{3}=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\\dfrac{10}{3}x=\dfrac{10}{3}\end{matrix}\right.\)
=>x=1 và y=0
=>A(1;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=\dfrac{10}{3}\cdot0-\dfrac{10}{3}=-\dfrac{10}{3}\end{matrix}\right.\)
=>\(B\left(0;-\dfrac{10}{3}\right)\)
O(0;0); A(1;0); B(0;-10/3)
=>\(OA=\sqrt{\left(1-0\right)^2+\left(0-0\right)^2}=1\)
\(OB=\sqrt{\left(0-0\right)^2+\left(-\dfrac{10}{3}-0\right)^2}=\dfrac{10}{3}\)
\(AB=\sqrt{\left(0-1\right)^2+\left(-\dfrac{10}{3}-0\right)^2}=\dfrac{\sqrt{109}}{3}\)
Vì \(OA^2+OB^2=AB^2\)
nên ΔOAB vuông tại O
Kẻ OH vuông góc AB tại H
=>OH là khoảng cách từ O đến (d)
Xét ΔOAB vuông tại O có OH là đường cao
nên \(OH\cdot AB=OA\cdot OB\)
\(\Leftrightarrow OH\cdot\dfrac{\sqrt{109}}{3}=1\cdot\dfrac{10}{3}\)
=>\(OH=\dfrac{10}{\sqrt{109}}\)
=>\(d\left(O;\left(d\right)\right)=\dfrac{10}{\sqrt{109}}\)
Cho đường thẳng d : y = (m + 2)x +2m - 6 ( m ≠ 2). Tính khoảng cách từ gốc tọa độ O cho đến đường thẳng d biết A(2;6) ∈ d