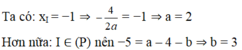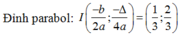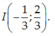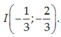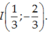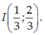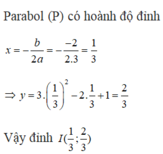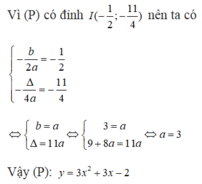Bài 1 :Cho parabol (P) : y = 2x + 4x parabol có đỉnh là :
A/ I(1;1)
B/ I (- 1;1)
C/ I ( -1;2)
D/ I ( 1;- 1)
Bài 2: Cho hàm số y= x-4 x + 4
a. Hàm số đồng biến trên (-∞;2) và nghịch biến trên (2;+∞)
b. Hàm số đồng biến trên (0;+∞) và nghịch biến trên(-∞;0)
c. Hàm số nghịch biến trên(-∞;2) và đồng biến (2;+∞)
Số phát biểu đúng là:
A. 0
B.1
C. 2
D.3
Bài 3: Cho hàm số y = \(\frac{1}{2}\)x- 2x -1 trong các điểm sau đây Điểm nào thuộc hàm số
A.M (2;3)
B. M (0;-1)
C. M (12;-12)
D. M (1;0)
Bài 4: trục đối xứng của (P): y= x+5x-1
A. X=5
B. X= \(-\frac{5}{2}\)
C. X=\(\frac{5}{2}\)
D. X=-5
Bài 5: giao điểm của (P): y= \(\frac{1}{2}x^2\)-21x-11 với trục tung là:
A. M( 0;2+\(\sqrt{2}\))
B. M(0;-11)
C. M(1;0)
D. M(\(2+\sqrt{2}\);0)
Bài 6: hàm số nào sau đây không phải đường thẳng
A. Y=3x-4
B. Y=5
C. Y= \(\sqrt{2}\) -1
D. Y=(x+1)(x-1)
Bài 7: giao điểm của (P): y=x +5x với trục hoành
A. (-2;3)
B. (0;0)và(-5;0)
C. (-5;0)
D. (0;0)và(0;-5)