Y = 4x2 (p) ; y = 3mx + 1 (d)
A) chứng minh d cắt (p) tại 2 điểm phân biệt về 2 phía oy
B) tìm m để d cắt (p) tại 2 điểm phân biệt
A (x1 ;y1 )
B (x2 ; y2 )
Sao cho : a) x1² + x2 2 = 8
b) 4 ( y1 - y2 ) = 15m
NH
Những câu hỏi liên quan
Rút gọn biểu thức sau: (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
(2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]
= [(2x)3 + y3] – [(2x)3 – y3]
= (2x)3 + y3 – (2x)3 + y3
= 2y3
Đúng 0
Bình luận (0)
1. Rút gọn biểu thức:
a. (2x-3)(4x2+6x+9)-2x(4x2-1)
b.(x+y)2+2(x+y)(x-y)+(x-y)2
2.Phân tích đa thức sau thành nhân tử:
a. 2x2y+4xy+2y c. x2-8x+7
b.9x2+6xy-4z2+y2 d. x3+4x2+x-6
1b.=2((x+y)+(x+y)(x-y)+(x-y))=2(x2-y2+x+y+x-y)=2(x2-y2+2x)=2x2-2y2+4x
2a.=4xy+4xy+2y=8xy+2y=2y(4x+1)
b.=(3x)2+2.3x.y+y2-(2z)2=(3x+y)2-(2z)2=(3x+y-2z)(3x+y+2z)
c.=x2-x-7x+7=x(x-1)-7(x-1)=(x-1)(x-7)
Đúng 0
Bình luận (0)
\(\left(x+y\right)^2+2\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\)
\(=\left(x+y+x-y\right)^2\)
\(=\left(2x\right)^2\)
\(=4x^2\)
hk tốt
^^
Đúng 0
Bình luận (0)
Rút gọn các biểu thức sau:
a) (x + 3)(x2 – 3x + 9) – (54 + x3)
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
a) (x + 3)(x2 – 3x + 9) – (54 + x3)
= ( x + 3)(x2 – 3.x + 32) – (54 + x3)
= x3 + 33 – (54 + x3)
= x3 + 27 – 54 – x3
= -27
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]
= [(2x)3 + y3] – [(2x)3 – y3]
= (2x)3 + y3 – (2x)3 + y3
= 2y3
Đúng 0
Bình luận (0)
a) (x + 3)(x2 – 3x + 9) – (54 + x3)
= ( x + 3)(x2 – 3.x + 32) – (54 + x3)
= x3 + 33 – (54 + x3) = x3 + 27 – 54 – x3
= -27
b) (2x + y)(4x2 – 2xy + y2) – (2x – y)(4x2 + 2xy + y2)
= (2x + y)[(2x)2 – 2x.y + y2] – (2x – y)[(2x)2 + 2x.y + y2]
= [(2x)3 + y3] – [(2x)3 – y3]
= (2x)3 + y3 – (2x)3 + y3
= 2y3
Đúng 0
Bình luận (0)
Cho hàm số
y
x
4
−
4
x
2
+
3
có đồ thị như hình vẽ. Tìm số cực trị của hàm số
y
x
4
−
4
x
2
+
3
A. 5 B. 6 C. 7 D. 3
Đọc tiếp
Cho hàm số y = x 4 − 4 x 2 + 3 có đồ thị như hình vẽ. Tìm số cực trị của hàm số y = x 4 − 4 x 2 + 3
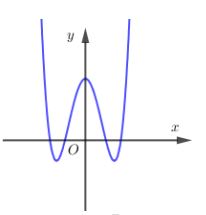
A. 5
B. 6
C. 7
D. 3
Đáp án A
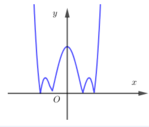
HD: Ta có: Giữ nguyên phần phía trên trục hoành, lấy đối xứng phần phía dưới trục hoành của đồ thị đã cho, ta được đồ thị hàm số y = x 4 − 4 x 2 + 3 ⇒ Hàm số có 7 cực trị.
Đúng 0
Bình luận (0)
bai 1 lam tinh chia (8x3-y3)(4x2-y2):(2x+y)(4x2-4xy+y2)
giup minh voi
Bài 1:
\(=\left(2x-y\right)\left(4x^2+2xy+y^2\right)\cdot\left(2x-y\right)\left(4x^2-4xy+y^2\right)\)
\(=\left(2x-y\right)^4\cdot\left(4x^2+2xy+y^2\right)\)
Đúng 0
Bình luận (0)
Đồ thị hàm số
y
4
x
2
+
4
x
+
3
−
4
x
2
+
1
có bao nhiêu đường tiệm cận ngang? A. 2 B. 0 C. 1 D. 3
Đọc tiếp
Đồ thị hàm số y = 4 x 2 + 4 x + 3 − 4 x 2 + 1 có bao nhiêu đường tiệm cận ngang?
A. 2
B. 0
C. 1
D. 3
Đáp án A
Ta có: y = 4 x + 2 4 x 2 + 4 x + 3 + 4 x 2 + 1 ⇒ lim x → + ∞ y = lim x → + ∞ 4 x + 2 4 x 2 + 4 x + 3 + 4 x 2 + 1
= lim x → + ∞ 4 + 2 x 4 + 4 x + 3 x 2 + 4 + 1 x 2 = 1 ⇒ y = 1 là TCN.
lim x → − ∞ = lim x → − ∞ = 4 x + 2 4 x 2 + 4 x + 3 + 4 x 2 + 1 = lim x → − ∞ − 4 − 2 x 4 + 4 x + 3 x 2 + 4 + 1 x 2 = − 1 ⇒ y = − 1 là TCN.
Vậy đồ thị hàm số có 2 đường TCN.
Đúng 0
Bình luận (0)
4x2-1
X(x+y)-6x-6y
X2-2xy+y2-z2
A2+2+2a+2ab+b2-ac-bc
9x2-1 phần 4
X2-2x-4y2-4y
9(x-y)2-4(x+y)2
(3x-2y)2-(2x-3y)2
9(x-y)2-4(x+y)2
\(4x^2-1=\left(2x-1\right)\left(2x+1\right)\)
\(x\left(x+y\right)-6x-6y=\left(x+y\right)\left(x-6\right)\)
\(x^2-2xy+y^2-z^2=\left(x-y-z\right)\left(x-y+z\right)\)
\(9x^2-\dfrac{1}{4}=\left(3x-\dfrac{1}{2}\right)\left(3x+\dfrac{1}{2}\right)\)
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
x
4
-
4
x
2
+
3
có đồ thị là đường cong trong hình vẽ bên. Hỏi phương trình
x...
Đọc tiếp
Cho hàm số y = f x = x 4 - 4 x 2 + 3 có đồ thị là đường cong trong hình vẽ bên. Hỏi phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có bao nhiêu nghiệm thực phân biệt?
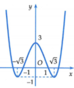
A. 9.
B. 10.
C.8.
D. 4
Chọn đáp án B
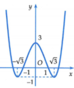
Ta có
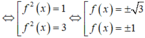
Quan sát đồ thị của hàm số y = f(x) ta thấy:
Phương trình f x = - 3 không có nghiệm; phương trình f x = - 1 có 2 nghiệm;
phương trình f x = 1 có 4 nghiệm; phương trình f x = 3 có 4 nghiệm.
Vậy phương trình x 4 - 4 x 2 + 3 2 - 4 x 4 - 4 x 2 + 3 2 + 3 = 0 có 10 nghiệm.
Đúng 0
Bình luận (0)
(Đề thi học sinh giỏi toán cấp 2, Miền Bắc năm 1963)Rút gọn và tính giá trị của biểu thức sau tại x -1,76 và y 3/25;
P
x
-
y
2
y
-
x
-...
Đọc tiếp
(Đề thi học sinh giỏi toán cấp 2, Miền Bắc năm 1963)
Rút gọn và tính giá trị của biểu thức sau tại x = -1,76 và y = 3/25;
P = x - y 2 y - x - x 2 + y 2 + y - 2 x 2 - x y - 2 y 2 : 4 x 2 + 4 x 2 y + y 2 - 4 x 2 + y + x y + x : x + 1 2 x 2 + y + 2
Thực hiện phép tính :
a) (4x2-5x2-3-3x2+9x) : (x2-3)
b) (4x2+4xy+y2) : (2x+y)
c) (x2-6xy+9y2) : (3y-x)
b) \(\left(4x^2+4xy+y^2\right):\left(2x+y\right)=\dfrac{\left(2x+y\right)^2}{2x+y}=2x+y\)
c) \(\left(x^2-6xy+9y^2\right):\left(3y-x\right)=\dfrac{\left(3y-x\right)^2}{3y-x}=3y-x\)
Đúng 2
Bình luận (0)