Cho p: y= x². Đường thẳng d có hệ số góc k và đi qua đierm M (0;1). Gọi 2 gdiem của d và p là A(x1; y1), B(x2; y2). Tìm k để tam giác OAB có diện tích = 2√2

Những câu hỏi liên quan
Cho parabol (P): y= -x2 và đường thẳng d đi qua điểm I(0; -1) có hệ số góc k. Viết phương trình đường thẳng (d).
Mục tiêu -500 sp mong giúp đỡ haha
Câu 3:
Cho hàm số y = x^2 có đồ thị (P) và đường thẳng (d) đi qua điểm M (1;2) có hệ số góc k ≠ 0.
Chứng minh rằng với mọi giá trị k khác 0. đường thẳng (d) luôn cắt (P) tại hai điểm phân biệt A và B.
Trong mặt phẳng Oxy, cho parabol P : y = -x 2 và đường thẳng d đi qua điểm M 0;-1 có hệ số góc k. c Viết phương trình đường thẳng d . Chứng minh rằng với mọi giá trị của ,k d luôn cắt P tại hai điểm phân biệt A,B. giúp mình nha
Cho hàm số y= -x2 có đồ thị (P). Gọi (d) là đường thẳng đi qua điểm M(0;1) và có hệ số góc k. Tìm điều kiện của k để đường thẳng d cắt đồ thị (P) tại 2 điểm phân biệt
Cho hàm số y= -x2 có đồ thị (P) và đường thẳng (d) có hệ số góc k≠0 đi qua điểm I (0;-1).Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt A và B
Gọi đường thẳng (d) có hàm số y=kx+b (k khác 0) (do hàm số có hệ số góc là k )
Vì (d) đi qua I(0;-1) => -1=0k+b => b=-1
=> y=kx-1(d)
Xét phương trình hoành độ giao điểm chung của (P) và (d) ta có:
-x^2=kx-1
<=> x^2-kx-1=0 (1)
Xét phương trình có a=1;c=-1 => ac=-1 <0
=> (1) luôn có 2 nghiệm phân biệt
=> (P) và (d) luôn cắt nhau tại 2 điểm phân biệt
Đúng 1
Bình luận (0)
Cho hàm số y= x2 +4x + 3
Đường thẳng (d) đi qua A(0;2) có hệ số góc k. Tìm k để (d) cắt (P) tại hai điểm E,F phân biệt sao cho trung điểm I của đoạn È nằm trên đường thẳng x-2y+3= 0
Đường thẳng (d) có dạng \(y=kx+m\)
\(A\left(0;2\right)\in\left(d\right)\Rightarrow m=2\)
\(\Rightarrow y=kx+2\left(d\right)\)
\(\left(d\right)\) cắt \(\left(P\right)\) tại hai điểm phân biệt khi phương trình \(x^2+\left(4-k\right)x+1=0\) có hai nghiệm phân biệt
\(\Leftrightarrow\Delta=\left(k-2\right)\left(k-6\right)>0\)
\(\Leftrightarrow\left[{}\begin{matrix}k>6\\k< 2\end{matrix}\right.\)
Ta có \(x_1=\dfrac{k-4+\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow E\left(\dfrac{k-4+\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4+k\sqrt{k^2-8k+12}}{2}\right)\)
\(x_1=\dfrac{k-4-\sqrt{k^2-8k+12}}{2}\Rightarrow y_1=\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\)
\(\Rightarrow F\left(\dfrac{k-4-\sqrt{k^2-8k+12}}{2};\dfrac{k^2-4k+4-k\sqrt{k^2-8k+12}}{2}\right)\)
Tọa độ trung điểm \(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\)
\(x-2y+3=0\left(d'\right)\)
\(I\left(\dfrac{k-4}{2};\dfrac{k^2-4k+4}{2}\right)\in\left(d'\right)\Rightarrow\dfrac{k-4}{2}-\left(k^2-4k+4\right)+3=0\)
\(\Leftrightarrow2k^2-9k+6=0\)
\(\Leftrightarrow\left[{}\begin{matrix}k=\dfrac{9+\sqrt{33}}{2}\left(l\right)\\k=\dfrac{9-\sqrt{33}}{2}\left(tm\right)\end{matrix}\right.\)
\(\Leftrightarrow k=\dfrac{9-\sqrt{33}}{2}\)
P/s: Không biết đúng kh.
Đúng 1
Bình luận (0)
Cho đường thẳng d có pt: 2kx + (3k-1)y - 6 = 0
a) Tìm đường thẳng d biết nó đi qua điểm A(-1;-3) và tìm hệ số góc của nó.
b) Tìm điểm B cố định mà d đi qua với mọi k.
trong mp tọa độ xOy ,cho Parabol (P) có pt y=-x2 và điểm M(0,-2)
a) viết pt đường thẳng (d) đi qua M với hệ số góc k (k thuộc R)
b) CM đườngthẳng (d) luôn cắt P tại 2 điểm phân biệt
c)XĐ k để đường thẳng (d) cắt Parabol tại A,B sao cho MA=2MB (A có hoành độ âm
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng
∆
:
x
-
1
2
y
+
1
1
z
-
1
. Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A
.
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho điểm M (2 ; 1 ; 0) và đường thẳng ∆ : x - 1 2 = y + 1 1 = z - 1 . Phương trình tham số của đường thẳng d đi qua M, cắt và vuông góc với Δ là:
A . d : x = 2 + t y = 1 - 4 t z = - 2 t
B . d : x = 2 - t y = 1 + t z = t
C . d : x = 1 + t y = - 1 - 4 t z = 2 t
D . d : x = 2 + 2 t y = 1 + t z = - t
Chọn A

Gọi I = d ∩ Δ. Do I ∈ Δ nên I (2t + 1; t – 1; -t).

từ đó suy ra d có một vectơ chỉ phương là ![]() và đi qua M (2 ; 1 ; 0) nên có phương trình
và đi qua M (2 ; 1 ; 0) nên có phương trình 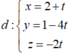
Đúng 0
Bình luận (0)
Cho đường thẳng d: y = (m + 2)x - 5 đi qua điểm có A(-1; 2). Hệ số góc của đường thẳng d là:
A. 1
B. 11
C. -7
D. 7
Đáp án C
Thay tọa độ điểm A vào phương trình đường thẳng d ta được
(m + 2).(-1) - 5 = 2 ⇔ -m - 2 = 7 ⇔ m = -9
Suy ra d: y = -7x - 5
Hệ số góc của đường thẳng d là k = -7
Đúng 0
Bình luận (0)




