a) Vẽ đồ thị của các hàm số y = 2x; y = 2x + 5; y = -2/3x và y = -2/3x + 5 trên cùng một mặt phẳng tọa độ.
b) Bốn đường thẳng trên cắt nhau tạo thành tứ giác OABC (O là gốc tọa độ). Tứ giác OABC có phải là hình bình hành không ? Vì sao ?
Bài 1 a) Khảo sát và vẽ đồ thị hàm số y=x³-2x²+x (C) b) từ đồ thị (C) suy ra đồ thị các hàm số sau: y=|x³-2x²+x|, y=|x|³ -2x²+|x| Bài 2: Khảo sát và vẽ đồ thị hàm số y=x⁴-2x²-3 (C). Từ đồ thị (C) suy ra đồ thị hàm số y=|y=x⁴-2x²-3|
Cho hàm số y=-2x+1 (d)
a) Vẽ đồ thị (d) của hàm số y=-2x+1
b) Xác định các hệ số a và b của hàm số y=ax+b, biết rằng đồ thị của hàm số này song song với đồ thị (d) và đi qua điểm A(2;1).
b: Vì (d1)//(d) nên (d1): y=-2x+b
=>a=-2
Thay x=2 và y=1 vào (d1), ta được:
b-4=1
=>b=5
a: 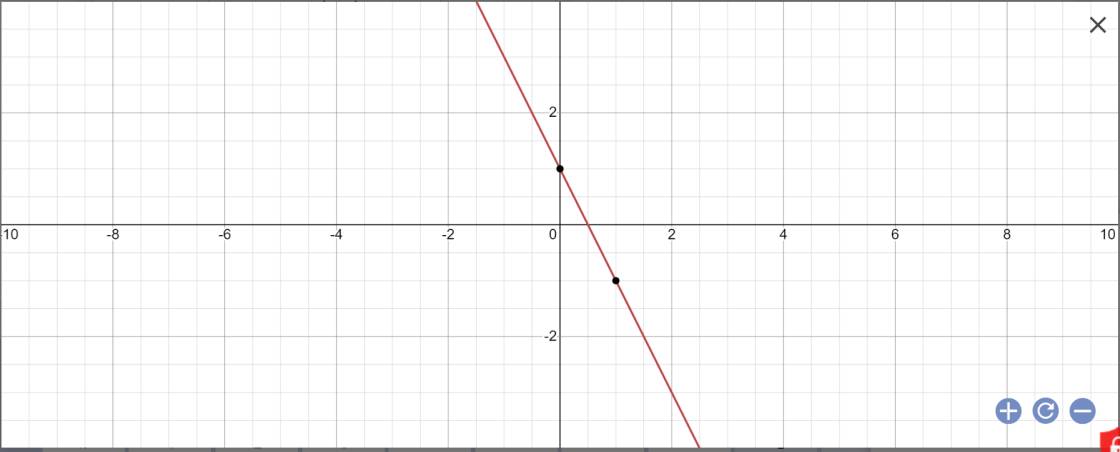
Vẽ đồ thị của hàm số y = -2x và vẽ đồ thị của hàm số y = 3x trên cùng một mặt phẳng toạ độ Oxy b) Xét xem các điểm M( 10; 15) ; N(-8 ;16), B(77;-14) điểm nào thuộc đồ thị hàm số y = - 2x
Câu 3: Cho các hàm số \(y=2x+5\) và \(y=-x+2\)
a. Vẽ đồ thị của hai hàm số đã cho trên cùng một mặt phẳng toạ độ Oxy.
b. Dựa vào hình vẽ, xác định toạ độ giao điểm A của hai đồ thị hàm số.
c. Hai đồ thị của hai hàm số đã cho cắt trục hoành tại các điểm B và C. Tính diện tích tam giác ABC
\(b,\text{PT hoành độ giao điểm: }2x+5=-x+2\Leftrightarrow3x=-3\\ \Leftrightarrow x=-1\Leftrightarrow y=3\Leftrightarrow A\left(-1;3\right)\\ c,\text{PT 2 đt giao Ox: }\left\{{}\begin{matrix}y=0\Rightarrow x=-\dfrac{5}{2}\Rightarrow B\left(-\dfrac{5}{2};0\right)\\y=0\Rightarrow x=2\Rightarrow C\left(2;0\right)\end{matrix}\right.\\ \Rightarrow BC=OB+OC=\dfrac{5}{2}+2=\dfrac{9}{2}\\ \text{Gọi H là chân đường cao từ A tới BC}\\ \Rightarrow AH=\left|y_A\right|=3\\ \Rightarrow S_{ABC}=\dfrac{1}{2}AH\cdot BC=\dfrac{1}{2}\cdot3\cdot\dfrac{9}{2}=\dfrac{27}{4}\left(đvdt\right)\)
Vẽ đồ thị của các hàm số sau:
a) y = 2x – 3;
b) y = -2x + 3.
a) y = 2x – 3
Bảng giá trị
| x | 0 | 3/2 |
| y = 2x – 3 | -3 | 0 |
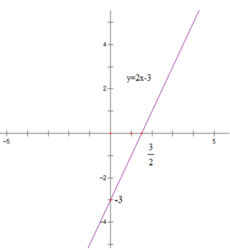
b) y = -2x – 3
Bảng giá trị
| x | 0 | (-3)/2 |
| y = -2x – 3 | -3 | 0 |
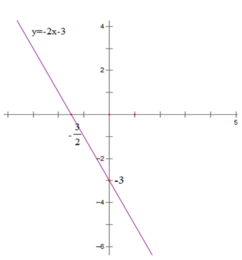
Vẽ đồ thị hàm số y= 2x
b) Xét xem các điểm A(1 ; 2), B( -1 ; 0) , C( 0.5 ; 1) có thuộc đồ thị hàm số
y= 2x không ?
Lời giải:
a.
b. Ta thấy:
$2=2.1$ hay $y_A=2x_A$ nên $A$ thuộc đths $y=2x$
$0\neq 2.(-1)$ hay $y_B\neq 2x_B$ nên $B$ không thuộc đths $y=2x$
$1=2.0,5$ hay $y_C=2x_C$ nên $C$ thuộc đths $y=2x$
cho hàm số y= -2x
a)vẽ đồ thị hàm số
b)cho các điểm B(-1;2) và C(-1,5;-3)
hỏi điểm nào thuộc đồ thị của hàm số y = -2x? vì sao?
a,cho y=1 suy ra x=-2
y=2 suy ra x=-4
b, Vì B(-1;2) suy ra x=-1 ; y=2
thay vào y=-2x
ta có 2=2 (luôn đúng )
suy ra Điểm B thuộc đồ thị hàm số
Vì C(-1,5;-3) x=-1,5,y=-3
thay vào ta được -3=3(vô lí)
suy ra A không thuộc đồ thị hàm số
mình vẽ hơi xấu thông cảm nha
nha
Cho đồ thị hàm số y = -2x
a) Vẽ thì bạn vẽ được ((:
b) B(-1;2)
Thay x = -1 ; y = 2 vào đồ thị hàm số ta có :
2 = (-2) . (-1) = 2 ( tmđb )
=> B thuộc đồ thị hàm số y = -2x
C(-1, 5; -3)
Thay x = -1, 5 ; y = -3 ta có :
( -2 ) . ( -1, 5 ) = 3 khác -3 ( vô lí )
=> C không thuộc đồ thị hàm số y = -2x
Cho hàm số: y = 2x + m -1 a) Tìm m để đồ thị của hàm số đi qua điểm A (2;2) Vẽ đồ thị của hàm số với giá trị của m vừa tìm được b) Tìm m để đồ thị của hàm số y = 2x + m – 1 cắt đồ thị của hàm số y = x + 1 tại điểm nằm trên trục hoành.
Cho hàm số y=-2x
a) Vẽ đồ thị của hàm số
b) Những điểm nào trong các điểm sau đây thuộc đồ thị của hàm số trên điểm A(-2;1) điểm B(-1;2)
a) cho x=1 => y=-2 khi đó ta được A(1;-2) (Có thể đặt điểm hoặc ko đặt vẫn được)
Vẽ đồ thị hàm số y=-2x là đường thẳng đi qua góc tọa độ (0;0) và A(1;-2)
Còn lại bạn vẽ như bình thường
b) -thay x=-2 vào hàm số y=-2x ta có y=-2.(-2)=4 ( không bằng tung độ của điểm A )
Vậy điểm A không thuộc đồ thị Y=-2x
- thay x=-1 vào đồ thị hàm số y=-2x ta có y=-2.(-1)=2 (bằng tung độ của điểm B)
Vậy điểm B thuộc đồ thị y=-2x
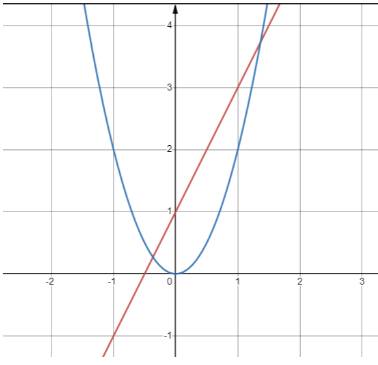
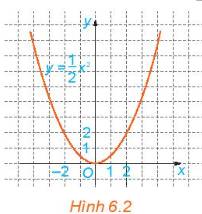
a) Dựa vào đồ thị của hàm số \(y=\dfrac{1}{2}x^2\)(H.6.2), tìm \(x\) sao cho \(y=8\).
b) Vẽ đồ thị của các hàm số \(y=2x+1\) và \(y=2x^2\) trên cùng một mặt phẳng tọa độ.
a) Để \(y = 8 \Leftrightarrow \frac{1}{2}{x^2} = 8 \Leftrightarrow {x^2} = 16 \Leftrightarrow x = 4\) hoăc \(x = - 4\)
b) Vẽ đồ thị y=2x+1:
-Là đồ thị bậc nhất nên đồ thị là đường thẳng đi qua điểm có tọa độ (0; 1) và
(-1; -1)
Vẽ đồ thị \(y = 2{x^2}\)
- Đi qua điểm (1; 2) ; (-1; 2);(0;0)