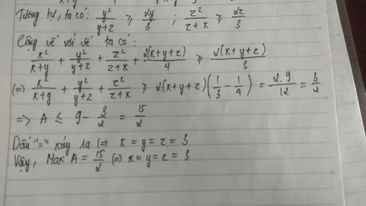Cho x,y,z thỏa mãn x+y+z=0; x+1>0; y+1>0 và z+4>0. Tìm GTLN của A=\(\frac{xy-1}{\left(x+1\right)\left(y+1\right)}+\frac{z}{z+4}\)
AJ
Những câu hỏi liên quan
cho x,y,z là các số thực dương thỏa mãn x,y,z>0 thỏa mãn x(x-z)+y(y-z) =0 tìm GTNN của \(P=\frac{x^3}{x^2+z^2}+\frac{y^3}{y^2+z^2}+\frac{x^2+y^2+4}{x+y}\)
\(x\left(x-z\right)+y\left(y-z\right)=0\)\(\Leftrightarrow\)\(x^2+y^2=z\left(x+y\right)\)
\(\frac{x^3}{z^2+x^2}=x-\frac{z^2x}{z^2+x^2}\ge x-\frac{z^2x}{2zx}=x-\frac{z}{2}\)
\(\frac{y^3}{y^2+z^2}=y-\frac{yz^2}{y^2+z^2}\ge y-\frac{yz^2}{2yz}=y-\frac{z}{2}\)
\(\frac{x^2+y^2+4}{x+y}=\frac{z\left(x+y\right)+4}{x+y}=z-x-y+\frac{4}{x+y}+x+y\ge z-x-y+4\)
Cộng lại ra minP=4, dấu "=" xảy ra khi \(x=y=z=1\)
cho x, y, z thỏa mãn x^3+y^3+3xyz<0 và z>0. chứng minh x+y<z
lllllllllllllllllllllllllllllllllllllllllllllllllllllll
Cho x,y,z ≠ 0 thỏa mãn: 2(x+y) = 3(y+z) = 4(x+z)
Tính P = \(\dfrac{x}{y}\)+\(\dfrac{y}{z}\)+\(\dfrac{z}{x}\)
Cho 3 số hữu tỉ x, y, z thỏa mãn với xyz(3x + y + z)(3y + z + x)(3z + x + y) \(\neq\) 0 thỏa mãn điều kiện \(\dfrac{x}{y+z+3x}=\dfrac{y}{z+x+3y}=\dfrac{z}{x+y+3z}\). Tính giá trị biểu thức:
A = \(\left(2+\dfrac{y+z}{x}\right)\left(2+\dfrac{z+x}{y}\right)\left(2+\dfrac{x+y}{z}\right)\)
Xét \(x+y+z=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}y+z=-x\\z+x=-y\\x+y=-z\end{matrix}\right.\)
\(\Rightarrow A=\left(2-1\right)\left(2-1\right)\left(2-1\right)=1\)
Xét \(x+y+z\ne0\) thì ta có:
\(\dfrac{x}{y+z+3x}=\dfrac{y}{z+x+3y}=\dfrac{z}{x+y+3z}=\dfrac{x+y+z}{5x+5y+5z}=\dfrac{x+y+z}{5\left(x+y+z\right)}=\dfrac{1}{5}\)
\(\Rightarrow\left\{{}\begin{matrix}5x=y+z+3x\\5y=z+x+3y\\5z=x+y+3z\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=y+z\\2y=z+x\\2z=x+y\end{matrix}\right.\)
\(\Rightarrow A=\left(2+2\right)\left(2+2\right)\left(2+2\right)=64\)
Vậy \(\left[{}\begin{matrix}A=1\\A=64\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Nếu bị lỗi thì bạn có thể xem đây nhé:

Đúng 1
Bình luận (1)
cho x,y,z >0 thỏa mãn x+y+z=9 Tìm max A=xy/x+y + yz/y+z + zx/z+x
Ta có:\(A=\dfrac{xy}{x+y}+\dfrac{yz}{y+z}+\dfrac{zx}{z+x}\)
\(=\dfrac{x\left(x+y\right)-x^2}{x+y}+\dfrac{y\left(y+z\right)-y^2}{y+z}+\dfrac{z\left(z+x\right)-z^2}{z+x}\)
\(=\left(x+y+z\right)-\left(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\right)\)
Ta có:\(\dfrac{x^2}{x+y}+\dfrac{x+y}{9}\ge2\sqrt{\dfrac{x^2}{x+y}.\dfrac{x+y}{9}}=\dfrac{2x}{3}\)
Tương tự,ta có:\(\dfrac{y^2}{y+z}+\dfrac{y+z}{9}\ge\dfrac{2y}{3};\dfrac{z^2}{z+x}+\dfrac{z+x}{9}\ge\dfrac{2z}{3}\)
Cộng vế với vế ta có:
\(\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}+\dfrac{2\left(x+y+z\right)}{4}\ge\dfrac{2\left(x+y+z\right)}{3}\)
\(\Leftrightarrow\dfrac{x^2}{x+y}+\dfrac{y^2}{y+z}+\dfrac{z^2}{z+x}\ge\dfrac{2\left(x+y+z\right)}{3}-\dfrac{2\left(x+y+z\right)}{4}=\dfrac{2.9}{3}-\dfrac{9}{2}=\dfrac{3}{2}\)
\(\Rightarrow A\le9-\dfrac{3}{2}=\dfrac{15}{2}\)
Dấu "=" xảy ra ⇔ x=y=z=3
Vậy,Max A=\(\dfrac{15}{2}\) ⇔ x=y=z=3
Đúng 0
Bình luận (0)
cho x,y,z khác 0 thỏa mãn 3x+y+z/x = x+3y+z/y = x+y+3z/z. Tính M= (x+y).(y+z).(z+y)/x.y.z
kkgkirtgkjssykjhskfsrlhklruwo8tiyfieusykdkwirkuiufysoiiyi
Đúng 0
Bình luận (0)
Tích trên có số thừa số:
(2012 - 2) : 10 + 1 = 202 (thừa số)
Cứ 4 thừa số thì đem lại cho ta tích có tận cùng là 6.
Mà 202 : 4 = 50 (dư 2)
Khi đó:
(2 x 12 x 22 x 32) x ... x (1962 x 1972 x 1982 x 1992) x 2002 x 2012
Vậy tận cùng của tích là: 6x2x2 có tận cùng là 4.
Câu 2:
Gọi ba số phải tìm là x,y,z
Ta có: x + y + z = 321,95 và 3x = 4y = 5z
Từ 3x = 4y = 5z
Cho ta:
x(13)=y(14)=z(15)=(x+y+z)(13+14...)x(13)=y(14)=z(15)=(x+y+z)(13+14...)(dãy tỉ số bằng nhau)
Do đó: x(13)=411→x=137x(13)=411→x=137
y = 102,75
z = 82,2
Vậy, .....
Đúng 0
Bình luận (0)
bay tào lao nhề phải là !@#$%^^*&&^^%^$##@!@#$$%
thế mới ngon lành độc lạ ko đụng hàng
Đúng 0
Bình luận (0)
Cho x ≥0; y ≥ 0; z ≥ 0 thỏa mãn x + y + z = 2. Tìm giá trị nhỏ nhất của biểu thức: P= x^2/y+z + y^2/x+z + z^2/x+y
Áp dụng bđt AM-GM ta có:
\(\frac{x^2}{x+y}+\frac{x+y}{4}\ge2\sqrt{\frac{x^2}{x+y}.\frac{x+y}{4}}=x\)
\(\frac{y^2}{x+z}+\frac{x+z}{4}\ge2\sqrt{\frac{y^2}{x+z}.\frac{x+z}{4}}\ge y\)
\(\frac{z^2}{x+y}+\frac{x+y}{4}\ge2\sqrt{\frac{z^2}{x+y}.\frac{x+y}{4}}\ge z\)
Cộng từng vế các bđt trên ta được:
\(P+\frac{x+y+z}{2}\ge x+y+z\)
\(\Rightarrow P\ge\frac{x+y+z}{2}=1\)
Dấu"="xảy ra \(\Leftrightarrow x=y=z=1\)
Vậy Min P=1 \(\Leftrightarrow x=y=z=1\)
anh Châu ơi, 1+1+1 đâu có = 2 anh.
à anh xl nhầm x=y=z=\(\frac{2}{3}\)
Xem thêm câu trả lời
cho x,y,z khác 0 thỏa mãn: 2( x+y)= 3(y+z)=4(z+x) tính
P= \(\dfrac{x}{y}+\dfrac{y}{z}+\dfrac{z}{x}\)
Lời giải:
$2(x+y)=3(y+z)=4(x+z)$
$\Rightarrow \frac{x+y}{6}=\frac{y+z}{4}=\frac{x+z}{3}$ (chia cả 3 vế cho $12$)
Đặt giá trị trên là $t$
$\Rightarrow x+y=6t; y+z=4t; z+x=3t$
$\Rightarrow x+y+z=(6t+4t+3t):2=6,5t$
$x=6,5t-4t=2,5t; y=6,5t-3t=3,5t; z=6,5t-6t=0,5t$. Khi đó:
$P=\frac{2,5t}{3,5t}+\frac{3,5t}{0,5t}+\frac{0,5t}{2,5t}$
$=\frac{2,5}{3,5}+\frac{3,5}{0,5}+\frac{0,5}{2,5}=\frac{277}{35}$
Đúng 0
Bình luận (0)
cho x,y,z khac 0 thỏa mãn x+y+z=2018 và x-2019y/z=y-2019z/x=z-2019x/y. Tìm x,y,z
cho x,y,z>0 thỏa mãn (x+y)(y+z)(z+x)=8xyz
chứng minh x=y=z