a: Phương trình có dạng ax+b=0 khi a<>0 được gọi là phương trình bậc nhất một ẩn

Phương trình 2x-5=2x+3 là phương trình bậc nhất một ẩn

c: Hai phương trình tương đương là hai phương trình có cùng tập nghiệm

a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn

Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên

b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn

c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn

Vì \( - {6.2^2} - 7.2 + 5 =  - 33 < 0\) nên \(x = 2\) không là nghiệm của bất phương trình trên

Phương trình bậc 2 một ẩn có dạng:

ax²+bx+c=0

Trong đó a,b,c là hệ số và là các số bất kì, x là ẩn và a phải khác 0 

Đúng thì tk nha

\(\Delta'=\left(-2m\right)^2-\left(4m^2-2\right)\)

\(=4m^2-4m^2+2\)

\(=2>0\forall0\)

Theo Vi - ét:

\(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1x_2=4m^2-2\end{matrix}\right.\)

\(x^2_1+4mx_2+4m^2-6=0\)

\(\Leftrightarrow x_1^2+\left(x_1+x_2\right)x_2+x_1x_2-4=0\)

\(\Leftrightarrow x_1^2+x_2^2+x_1x_2+x_1x_2-4=0\)

\(\Leftrightarrow\left(x_1+x_2\right)^2=4\)

\(\Leftrightarrow\left(4m\right)^2=4\)

\(\Leftrightarrow\left|4m\right|=2\)

\(\Leftrightarrow\left[{}\begin{matrix}4m=2\\4m=-2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}m=\dfrac{1}{2}\\m=-\dfrac{1}{2}\end{matrix}\right.\)

Vậy với \(m=\left\{\dfrac{1}{2};-\dfrac{1}{2}\right\}\) thì pt có 2 nghiệm x₁,x₂ thỏa mãn biểu thức ...

Đáp án là C

a) Ví dụ:

\(\begin{array}{l}{x^2} - x + 1 > 0\\ - {x^2} + 5x + 5 \le 0\end{array}\)

b)

Bất phương trình bậc nhất: \(x - 1 > 0\)

Bất phương trình hai ẩn: \(2x + y < 5\)

x 2  - (m + 1)x + m – 2 = 0 (1)

a) Δ = m + 1 2  - 4(m – 2) = m 2  + 2m + 1 – 4m + 8

=  m 2  - 2m + 9 = m - 1 2  + 8 > 0 với mọi m.

Vậy với mọi m thuộc R, thì phương trình (1) luôn luôn có hai nghiệm phân biệt x 1  và  x 2

x 2 - 2mx + 2m – 1 = 0

Δ = b 2  - 4ac = 2 m 2  - 4.(2m - 1) = 4 m 2  -8m + 4 = 4 m - 1 2

Do Δ = 4 m - 1 2 ≥ 0 ∀ m nên phương trình luôn có nghiệm với mọi m

Bước 1: Mở trang Geoebra

Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).

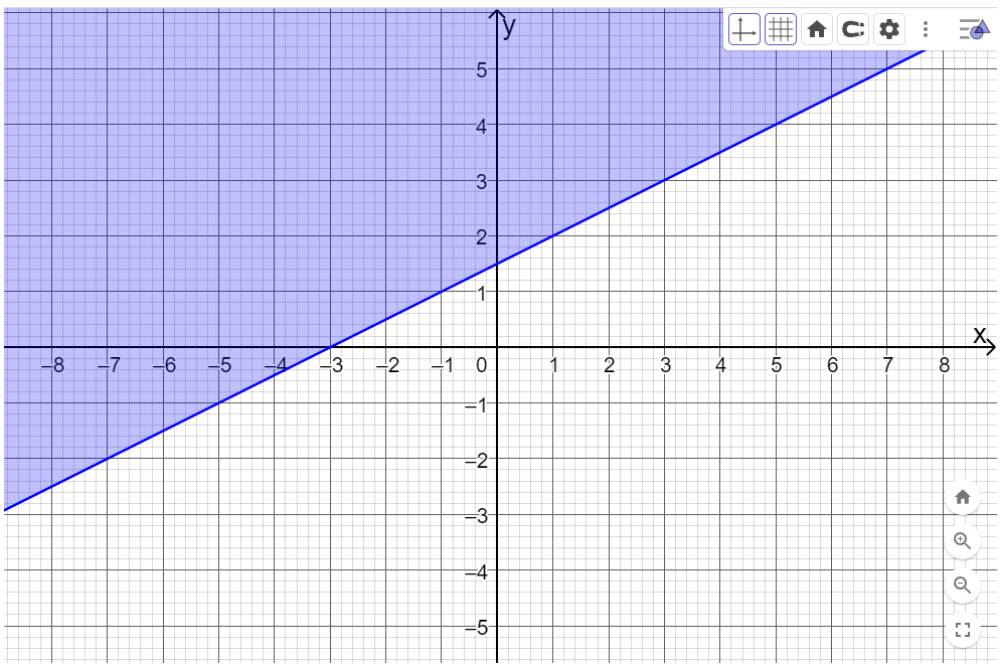
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:

x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.

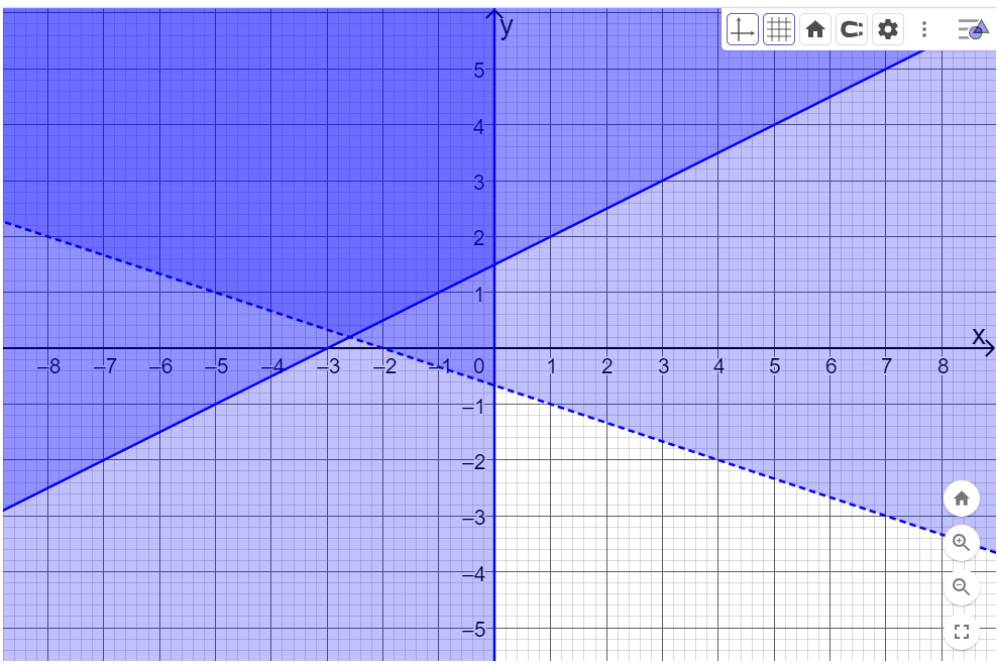
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y =  - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.