Cho phương trình bậc hai: x 2 – 5x – 2 = 0. Không giải phương trình để tìm 2 nghiệmx1 ; x2 . Hãy tính giá trị của biểu thức: A =x1−1x2−1+x2−1x1−1
TT
Những câu hỏi liên quan
Cho phương trình bậc hai: x 2 – 5x – 2 = 0. Không giải phương trình để tìm 2 nghiệmx1 ; x2 . Hãy tính giá trị của biểu thức: A =\(\dfrac{x1-1}{x2-1}+\dfrac{x2-1}{x1-1}\)
Cho phương trình bậc hai: x²-( 2m+3)x +m²+2=0.
1. Tìm m để phương trình có hai nghiệm phân biệt.
2. Không giải phương trình, tìm m để phương trình có nghiệm này bằng 3 lần nghiệm kia.
cho phương trình : x^2 + 5x - 1 = 0 ( 1 )
Không giải phương trình ( 1 ), hãy lập 1 phương trình bậc hai có các nghiệm là lũy thừa bậc bốn của các nghiệm của phương trình ( 1 )
Gọi x1,x2 là các nghiệm của phương trình đã cho
Áp dụng hệ thức Vi-et,ta có :
x1 + x2 = -5 ; x1x2 = -1
gọi y1,y2 là các nghiệm của phương trình phải lập,ta được :
y1 + y2 = x14 + x24 , y1y2 = x14x24
Ta có : x12 + x22 = ( x1 + x2 )2 - 2x1x2 = 25 + 2 - 27
Do đó : y1 + y2 = x14 + x24 = ( x12 + x22 )2 - 2x12x22 = 729 - 2 = 727
y1y2 = ( x1x2 )4 = 1
Từ đó pt phải lập có dạng : y2 - 727y + 1 = 0
Ta co: P = -1 <0
=> (1) có 2 nghiệm phân biệt khác dấu
Gọi hai nghiệm đó là \(x_1;x_2\)
=> \(x_1+x_2=-5;x_1.x_2=-1\)
Ta có: \(\left(x_1.x_2\right)^4=\left(-1\right)^4=1\)
\(\left(x_1\right)^4+\left(x_2\right)^4=\left(x_1^2+x_2^2\right)^2-2x_1^2x_2^2=\left[\left(x_1+x_2\right)^2-2x_1x_2\right]^2-2x_1^2x_2^2\)
\(=\left[\left(-5\right)^2-2.\left(-1\right)\right]^2-2.\left(-1\right)^2\)
\(=727\)
=> Phương trình có các nghiệm lũy thừa bậc 4 của các nghiệm phương trình (1) là:
\(x^2-727x+1=0\)
(1) Cho phương trình bậc hai ẩn x ( m là tham số)x^2-4x+m=0(1) a) Giải phương trình với m =3 b) Tìm đk của m để phương trình (1) luôn có 2 nghiệm phân biệt (2) Cho phương trình bậc hai x^2-2x -3m+1=0 (m là tham số) (2) a) giải pt với m=0 b)Tìm m để pt (2) có nghiệm phân biệt. ( mng oii giúp mk vs mk đang cần gấp:
Bài 1:
a) Thay m=3 vào (1), ta được:
\(x^2-4x+3=0\)
a=1; b=-4; c=3
Vì a+b+c=0 nên phương trình có hai nghiệm phân biệt là:
\(x_1=1;x_2=\dfrac{c}{a}=\dfrac{3}{1}=3\)
Đúng 1
Bình luận (0)
Bài 2:
a) Thay m=0 vào (2), ta được:
\(x^2-2x+1=0\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
hay x=1
Đúng 1
Bình luận (0)
Giải bài tập phương trình bậc hai.
Bài 1. Tìm điều kiện của m để phương trình sau có nghiệm:
2x^2 + 3x +2m - 1 = 0
Bài 2. Cho phương trình (m - 4)x^2 - 2xm+ m - 2 = 0
a) Giải phương trình với m = 6
b) Tìm m để phương trình có nghiệm là Căn 2
c) Tìm m để phương trình có nghiệp kép, 2 nghiệm phân biệt, nghiệm duy nhất.
Xem chi tiết
Dùng công thức nghiệm của phương trình bậc hai để giải các phương trình sau:
3x2 + 5x + 2 = 0
Phương trình bậc hai 3x2 + 5x + 2 = 0
Có a = 3; b = 5; c = 2; Δ = b2 – 4ac = 52 – 4.3.2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
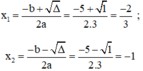
Vậy phương trình có hai nghiệm là -1 và 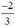
Đúng 0
Bình luận (0)
Cho phương trình: x2 + 5x – 1=0 (1)
Không giải phương trình,hãy lập một phương trình bậc hai có các nghiệm là lũy thừa bậc bốn của các nghiệm phương trình (1)
Cho phương trình \(\sqrt {{x^2} - 3x + 2} = \sqrt { - {x^2} - 2x + 2} \)
a) Bình phương hai vế của phương trình để khử căn và giải phương trình bậc hai nhận được
b) Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không
a) Bình phương hai vế của phương trình\(\sqrt {{x^2} - 3x + 2} = \sqrt { - {x^2} - 2x + 2} \)ta được:
\({x^2} - 3x + 2 = - {x^2} - 2x + 2\)(1)
Giải phương trình trên ta có:
\((1) \Leftrightarrow 2{x^2} - x = 0\)
\( \Leftrightarrow x(2x - 1) = 0\)
\( \Leftrightarrow x = 0\) hoặc \(x = \frac{1}{2}\)
b) Thử lại ta có:
Với x=0, thay vào phương trình đã cho ta được: \(\sqrt {{0^2} - 3.0 + 2} = \sqrt { - {0^2} - 2.0 + 2} \Leftrightarrow \sqrt 2 = \sqrt 2 \) (luôn đúng)
Với \(x = \frac{1}{2}\), thay vào phương trình đã cho ta được:
\(\sqrt {{{\left( {\frac{1}{2}} \right)}^2} - 3.\frac{1}{2} + 2} = \sqrt { - {{\left( {\frac{1}{2}} \right)}^2} - 2.\frac{1}{2} + 2} \Leftrightarrow \sqrt {\frac{3}{4}} = \sqrt {\frac{3}{4}} \) (luôn đúng)
Vậy các giá trị x tìm được ở câu a thỏa mãn phương trình đã cho.
Đúng 0
Bình luận (0)
cho phương trình:x2-2m.(m-2).x+2m-5=0
a)chứng minh phương trình luôn có 2 nghiệm phân biệt ∀
b) tìm m để có nghiệm phương trình nhỏ hơn 1
c)tìm m để phương trình có 2 nghiệmx1;x2 thỏa mãn x1 -3x2=m




