Tìm hai số u và v trong trường hợp : u\(^2\)+v\(^2\)=13; u.v=6
NV
Những câu hỏi liên quan
Tìm hai số u, v trong mỗi trường hợp sau:
a) u + v = \(3\sqrt{2}\) và u.v =4
b) u - v = -2 và u.v = 80
c) \(u^2+v^2\) = 13 và u.v = 16
a) Vì \(u+v=3\sqrt{2}\) và uv=4
nên u,v là hai nghiệm của phương trình: \(x^2-3\sqrt{2}x+4=0\)
\(\Delta=\left(-3\sqrt{2}\right)^2-4\cdot1\cdot4=18-16=2>0\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{3\sqrt{2}-\sqrt{2}}{2}=\sqrt{2}\\x_2=\dfrac{3\sqrt{2}+\sqrt{2}}{2}=2\sqrt{2}\end{matrix}\right.\)
Vậy: \(u=\sqrt{2};v=2\sqrt{2}\)
Đúng 2
Bình luận (0)
Tìm hai số u,v trong mỗi trường hợp sau:
a) u+v = 29 và u.v = 198
b) u+v = \(3\sqrt{2}\) và u.v = 4
c) u-v = -2 và u.v = -80
d) \(u^2+v^2=13\) và u.v = 6
a) Vì u+v=29 và uv=198 nên u,v là hai nghiệm của phương trình:
\(x^2-29x+198=0\)
\(\Leftrightarrow x^2-18x-11x+198=0\)
\(\Leftrightarrow x\left(x-18\right)-11\left(x-18\right)=0\)
\(\Leftrightarrow\left(x-18\right)\left(x-11\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-18=0\\x-11=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=18\\x=11\end{matrix}\right.\)
Vậy: u=18; v=11
Đúng 1
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
u + v = 2, uv = 9
S = 2 ; P = 9 ⇒ S2 – 4P = 22 – 4.9 = -32 < 0
⇒ Không tồn tại u và v thỏa mãn.
Đúng 0
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
a) u + v = 32 , uv = 231
b) u + v = -8, uv = -105
c) u + v = 2, uv = 9
a) S = 32 ; P = 231 ⇒ S 2 – 4 P = 322 – 4 . 231 = 100 > 0
⇒ Tồn tại u và v là hai nghiệm của phương trình: x 2 – 32 x + 231 = 0 .
Ta có: Δ = ( - 32 ) 2 – 4 . 231 = 100 > 0
⇒ PT có hai nghiệm:
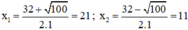
Vậy u = 21 ; v = 11 hoặc u = 11 ; v = 21.
b) S = -8; P = -105 ⇒ S 2 – 4 P = ( - 8 ) 2 – 4 . ( - 105 ) = 484 > 0
⇒ u và v là hai nghiệm của phương trình: x 2 + 8 x – 105 = 0
Ta có: Δ ’ = 4 2 – 1 . ( - 105 ) = 121 > 0
Phương trình có hai nghiệm:
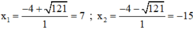
Vậy u = 7 ; v = -15 hoặc u = -15 ; v = 7.
c) S = 2 ; P = 9 ⇒ S 2 – 4 P = 2 2 – 4 . 9 = - 32 < 0
⇒ Không tồn tại u và v thỏa mãn.
Đúng 0
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
u + v = 12, uv = 28 và u > v
S = 12, P = 28 ⇒ S2 – 4P = 32 > 0
⇒ u, v là hai nghiệm của phương trình: x2 – 12x + 28 = 0.
Có a = 1; b = -12; c = 28 ⇒ Δ’ = (-6)2 – 28 = 8 > 0
Phương trình có hai nghiệm x1 = 6 + 2√2; x2 = 6 - 2√2
Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2
Đúng 0
Bình luận (0)
Tìm hai số u và v trong mỗi trường hợp sau:
a) u + v = 12, uv = 28 và u > v
b) u + v = 3, uv = 6
a) S = 12, P = 28 ⇒ S 2 – 4 P = 32 > 0
⇒ u, v là hai nghiệm của phương trình: x 2 – 12 x + 28 = 0 .
Có a = 1; b = -12; c = 28 ⇒ Δ ’ = ( - 6 ) 2 – 28 = 8 > 0
Phương trình có hai nghiệm x 1 = 6 + 2 √ 2 ; x 2 = 6 - 2 √ 2
Vì u > v nên u = 6 + 2√2 và v = 6 - 2√2
b) S = 3; P = 6 ⇒ S 2 – 4 P = - 15 < 0
Vậy không tồn tại u, v thỏa mãn yêu cầu.
Đúng 0
Bình luận (0)
tìm hai số u và v trong mỗi trường hợp sau : a) u+v=32,v .u=231
H = 32; U = 231 => H^2 - 4U = 32^2 - 4.231 = 100 > 0
tồn tại u và v là 2 nghiệm pt: x^2 - 32x + 231 = 0
ta có: \(\Delta=\left(-32x\right)^2-4.231=100>0\)
pt có 2 nghiệm:
\(x_1=\frac{32+100}{2.1}=21;x_2=\frac{32-\sqrt{100}}{2.1}=11\)
\(\Rightarrow\hept{\begin{cases}u=21;v=11\\u=11;v=21\end{cases}}\)
4. Nêu cách tìm hai số, biết tổng S và tích P của chúng.Tìm hai số u và v trong mỗi trường hợp sau:
a
)
u
+
v
3
u
v
−
8
b
)
u
+
v...
Đọc tiếp
4. Nêu cách tìm hai số, biết tổng S và tích P của chúng.
Tìm hai số u và v trong mỗi trường hợp sau:
a ) u + v = 3 u v = − 8 b ) u + v = − 5 u v = 10
Tìm hai số u và v trong mỗi trường hợp sau:
u + v = 42, uv = 441
S = 42; P = 441 ⇒ S2 – 4P = 422 – 4.441 = 0
⇒ u và v là hai nghiệm của phương trình: x2 – 42x + 441 = 0
Có: Δ’ = (-21)2 – 441 = 0
⇒ Phương trình có nghiệm kép x1 = x2 = -b’/a = 21.
Vậy u = v = 21.
Đúng 0
Bình luận (0)



