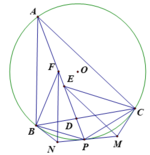
Cho (O) nội tiếp ΔABC cân tại A. Tiếp xúc các cạnh AB,BC,CA tại D,E,F; tia BF cắt điểm O tại I. CMinh
a) DF//BC và BDFC nội tiếp được đường tròn
b) IB^2=IP.ID
c) IB=IE
d) Diện tích ΔDBI = diện tích Δ DIE
TT
Những câu hỏi liên quan
cho ΔABC nội tiếp đường tròn tâm (O) , (O') tiếp xúc các cạnh AB , AC tại E và F. (O') tiếp xúc với (O) tại S. gọi I là tâm của đường tròn nội tiếp ΔABC
chứng minh : BEIS , CFIS nội tiếp.
Cho đường tròn tâm O nội tiếp tam giác ABC tiếp xúc với các cạnh BC,CA,AB tương ứng tại D,E,F. Đường tròn tâm O bàng tiếp góc BAC của tam giascABC tiếp xúc với BC và phần kéo dài của các cạnh AB,AC tại P,M,N1. Chứng minh rằng BPCD2. Trên đường thẳng MN lấy các điểm I và K sao cho CK // AB, BI//AC .Chứng minh rằng các tứ giác BICE và BKCF là các hình bình hành.3. Gọi (S) là đường tròn đi qua ba điểm I,K,P. Chứng minh (S) tiếp xúc với các đường thẳng BC,BI,CK
Đọc tiếp
Cho đường tròn tâm O nội tiếp tam giác ABC tiếp xúc với các cạnh BC,CA,AB tương ứng tại D,E,F. Đường tròn tâm O' bàng tiếp góc BAC của tam giascABC tiếp xúc với BC và phần kéo dài của các cạnh AB,AC tại P,M,N
1. Chứng minh rằng BP=CD
2. Trên đường thẳng MN lấy các điểm I và K sao cho CK // AB, BI//AC .Chứng minh rằng các tứ giác BICE và BKCF là các hình bình hành.
3. Gọi (S) là đường tròn đi qua ba điểm I,K,P. Chứng minh (S) tiếp xúc với các đường thẳng BC,BI,CK
Cho tam giác ABC. Đường tròn nội tiếp tiếp xúc với các cạnh BC, CA và AB tại D, E và F. M
là điểm bất kì nằm trong tam giác sao cho đường tròn nội tiếp tam giác MBC tiếp xúc với BC tại
D và tiếp xúc cạnh MB và MC tại N, P. CMR tứ giác NPEF nội tiếp.
cho tam giác ABC vuông tại A có AB=1/2BC.Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với Các cạnh BC,CA,AB lần lượt tại D,E,F.
CMR : sdFE : sdFD : sdDE =3:4:5
Cho tam giác ABC ( AB=AC). Cạnh AB,BC,CA tiếp xúc với đường tròn (O) tại các điểm D,E,F . BF cắt O tại I, DI cắt BC tại M. CM
a) Tam giác DEF có ba góc nhọn
b) DF//BC
c) Tứ giác BDFC nội tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). Đường tròn (J) bàng tiếp góc A tiếp xúc với các đường thẳng BC, CA, AB lần lượt tại D, E, F. Gọi M là trung điểm của BC. Đường tròn đường kính MJ cắt DE tại điểm K khác D. Gọi D là giao điểm thứ hai của đường thẳng AD và (J) .
a) Chứng minh rằng bốn điểm B, D, K, D cùng nằm trên một đường tròn.
b) Gọi G là giao của BC và EF, đường thẳng GJ cắt AB, AC lần lượt tại L và N. Lấy các điểm P, Q lần lượt trên các đường thẳng JB, JC sao cho...
Đọc tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). Đường tròn (J) bàng tiếp góc A tiếp xúc với các đường thẳng BC, CA, AB lần lượt tại D, E, F. Gọi M là trung điểm của BC. Đường tròn đường kính MJ cắt DE tại điểm K khác D. Gọi D là giao điểm thứ hai của đường thẳng AD và (J) .
a) Chứng minh rằng bốn điểm B, D, K, D' cùng nằm trên một đường tròn.
b) Gọi G là giao của BC và EF, đường thẳng GJ cắt AB, AC lần lượt tại L và N. Lấy các điểm P, Q lần lượt trên các đường thẳng JB, JC sao cho \(\widehat{PAB}=\widehat{QAC}=90^o\). Các đường thẳng LP và NQ cắt nhau tại T. Gọi S là điểm chính giữa cung BAC của (O) và T là giao của AT với (O). Chứng minh rằng đường thẳng ST' đi qua tâm đường tròn nội tiếp tam giác ABC.
Cho tam giác ABC (không cân) nội tiếp đường tròn (O). Các tiếp tuyến với đường tròn (O) tại A, B, C lần lượt cắt BC, CA, AB tại D, E, F. CMR: D, E, F thẳng hàng
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F. Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M. Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N. 1) Chứng minh rằng đường thẳng MN tiếp xúc với (O).
Đọc tiếp
Cho tam giác ABC nhọn không cân nội tiếp đường tròn (O). D là điểm thuộc cạnh BC (D khác B và D khác C).
Trung trực của CA; AB lần lượt cắt đường thẳng AD tại E, F.
Đường thẳng qua E song song với AC cắt tiếp tuyến qua C của (O) tại M.
Đường thẳng qua F song song với AB cắt tiếp tuyến qua B của (O) tại N.
1) Chứng minh rằng đường thẳng MN tiếp xúc với (O).
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.
Đúng 0
Bình luận (0)
cho tam giác cân ABC ( AB=AC), các cạnh AB,BC,CA tiếp xúc với đường tròn (O) tại các điểm tương ứng D,E,F,BF cắt đường tròn (O) tại điểm thứ hai là I, tia DI cắt BC tại M. chứng minh EC^2 =ME.CB
Cho đường tròn ( O ) nội tiếp tam giác cân ABC. Đường tròn (O) tiếp xúc với các cạnh AB, BC, CA lần lượt tại D, E, F
a, BF cắt (O) tại P. Gọi I là giao điểm DP và BC Chứng minh rằng: IEP ~ IDE ; IBF ~ IDB
b, So sánh diện tích tam giác IDE và diện tích tam giác IDB


