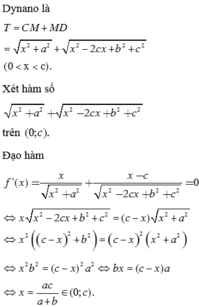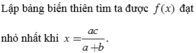Từ hai vị trí quan sát A và B của một tòa nhà; người ta quan sát đỉnh C của ngọn núi. Biết rằng độ cao AB = 70m, phương nhìn AC tạo với phương nằm ngang một góc 30°, phương nhìn BC tạo với phương nằm ngang một góc 15°30' . Tính chiều cao của ngọn núi
TN
Những câu hỏi liên quan
Một người quan sát đỉnh một tòa nhà tại hai vị trí cách nhau 12m với các góc nâng là 0 20 và 0 35 (xem hình). Hỏi chiều cao của tòa nhà là bao nhiêu? (làm tròn đến chữ số thập phân thứ hai)
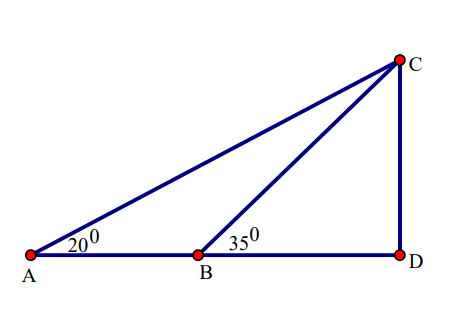
Hai vị trí cách nhau 12m tức là \(AB=12\left(m\right)\)
Ta có \(\tan\widehat{A}=\dfrac{CD}{AD}=\tan20^0\approx0,4\Leftrightarrow AD=\dfrac{CD}{0,4}\)
\(\tan\widehat{CBD}=\dfrac{CD}{BD}=\tan35^0\approx0,7\Leftrightarrow BD\approx\dfrac{CD}{0,7}\)
Ta có \(AD-BD=AB=12\)
\(\Leftrightarrow\dfrac{CD}{0,4}-\dfrac{CD}{0,7}=12\Leftrightarrow CD=\dfrac{56}{5}=11,2\left(m\right)\)
Vậy...
Đúng 1
Bình luận (0)
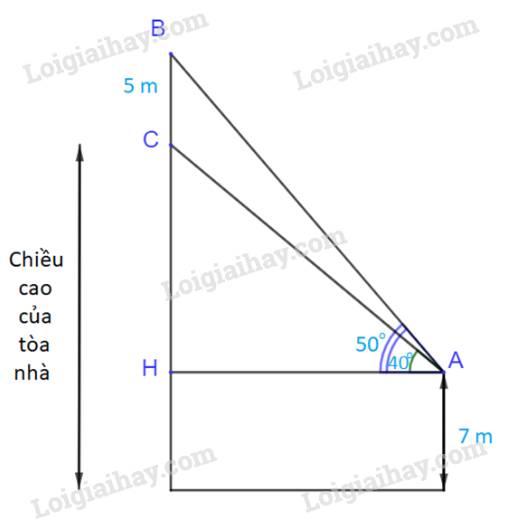
trên nóc 1 tòa nhà có một cột ăng - ten cao 5m . Từ vị trí quan sát A cao 7m so với mặt đất , có thể nhìn thấy đỉnh B và chân C của cột ăng - ten dưới góc 500 và 400 so với phương nằm ngang . Tính chiều cao của tòa nhà
ve hinh thang vuong ABED co AD//BC ; va ED vuong goc voi BC keo dai ;
E thuoc BC keo dai(hinh chieu cua BC tren mat dat)
.D la diem duoi mat dat cua A AD=7m; BC=5m
Cac goc 40 ; 50 do la giua AC ; AB voi phuong nam ngang .
Ta tinh duoc DE theo BC : DE =BC/(tan50-tan40)
=> Bc da biet tan ta tra duoc .Con CE la chieu cao cua nha :
Vay : CE=AD+DE*tan40= 7+5*tan40/(tan50-tan40)
Đúng 0
Bình luận (0)
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là {45^o} và {75^o}. Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Đọc tiếp
Một người đi dọc bờ biển từ vị trí A đến vị trí B và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là \({45^o}\) và \({75^o}\). Biết khoảng cách giữa hai vị trí A, B là 30 m (Hình 32). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
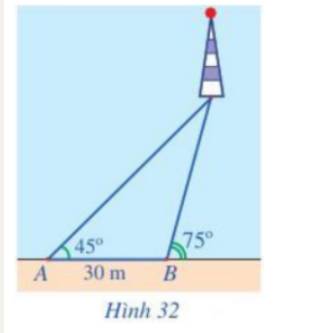
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên AB.
Khi đó CH là khoảng cách từ ngọn hải đăng tới bờ biển.
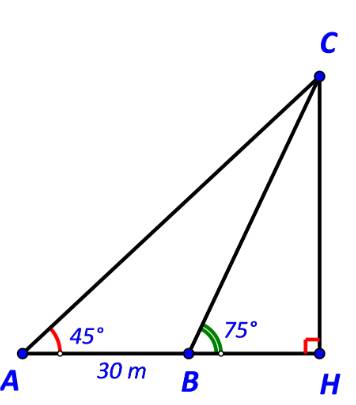
Ta có: \( \widehat {ACB} = \widehat {HBC} - \widehat {BAC} = {75^o} - {45^o} = {30^o}; \, \widehat {ABC} = {180^o} - {75^o} = {105^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\)
\( \Rightarrow AC = \sin B.\frac{{AB}}{{\sin C}} = \sin {105^o}.\frac{{30}}{{\sin {{30}^o}}} \approx 58\)
Tam giác ACH vuông tại H nên ta có:
\(CH = \sin A.AC = \sin {45^o}.58 \approx 41\)
Vậy ngọn hải đăng cách bờ biển 41 m.
Đúng 0
Bình luận (0)
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là {50^o}và {40^o} so với phương nằm ngang (H.3.18).a) Tính các góc của tam giác ABC.b) Tính chiều cao của tòa nhà.
Đọc tiếp
Trên nóc một tòa nhà có một cột ăng-ten cao 5m. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh B và chân C của cột ăng-ten, với các góc tương ứng là \({50^o}\)và \({40^o}\) so với phương nằm ngang (H.3.18).
a) Tính các góc của tam giác ABC.
b) Tính chiều cao của tòa nhà.
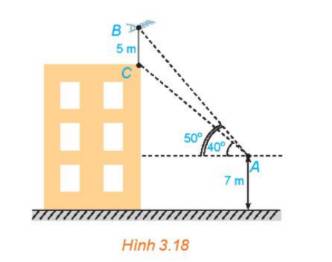
Tham khảo:
a)
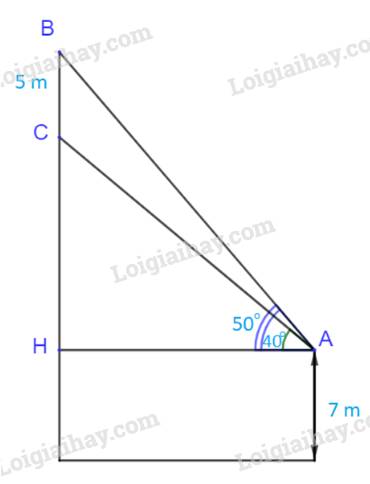
Gọi H là hình chiếu của A lên đường thẳng BC.
Ta có: \(\widehat {HAB} = {50^o}\); \(\widehat {HAC} = {40^o}\)
\( \Rightarrow \widehat {BAC} = {50^o} - {40^o} = {10^o}\) (1)
Xét tam giác ABH, vuông tại H ta có:
\(\widehat H = {90^o};\;\widehat {BAH} = {50^o}.\)
\( \Rightarrow \widehat {HBA} = {180^o} - {90^o} - {50^o} = {40^o}\) hay \(\widehat {CBA} = {40^o}\). (2)
Từ (1) và (2), suy ra: \(\widehat {BCA} = {180^o} - {40^o} - {10^o} = {130^o}.\)
Vậy ba góc của tam giác ABC lần lượt là: \(\widehat A = {10^o};\;\widehat B = {40^o};\;\widehat C = {130^o}\).
b)
Áp dụng định lý sin cho tam giác ABC, ta được:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}}\) \( \Rightarrow AB = \frac{{BC.\sin C}}{{\sin A}}\)
Mà: \(BC = 5\;(m);\;\;\widehat C = {130^o};\;\widehat A = {10^o}\)
\( \Rightarrow AB = \frac{{5.\sin {{130}^o}}}{{\sin {{10}^o}}} \approx 22\;(m)\)
Xét tam giác ABH, vuông tại H ta có:
\(\sin \widehat {BAH} = \frac{{BH}}{{AB}}\)\( \Rightarrow BH = AB.\,\,\sin \widehat {BAH}\)
Mà: \(AB \approx 22\;(m);\;\;\widehat {BAH} = {50^o}\)
\( \Rightarrow BH \approx 22.\sin {50^o} \approx 16,85\;(m)\)
Vậy chiều cao của tòa nhà là: \(BH-{\rm{ }}BC + 7 = 16,85-5 + 7 = 18,85{\rm{ }}\left( m \right)\)
Đúng 0
Bình luận (0)
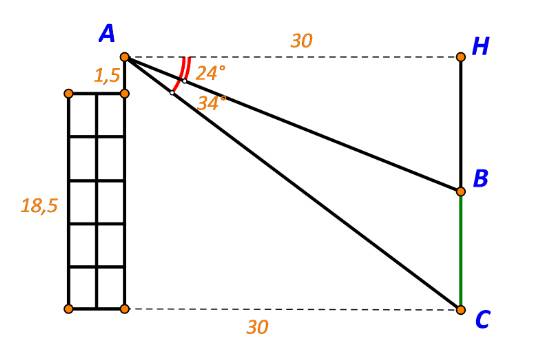
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là \({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là \({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Gọi A là vị trí đứng của Nam, B là điểm cao nhất của cây, C là vị trí gốc cây.
Gọi H là hình chiếu của A trên BC. Ta có hình vẽ:
TH1: Cây cao hơn tòa nhà

Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = BH + HC \approx 13,357 + 1,5 + 18,5 = 33,357(m)\)
TH2: Cây thấp hơn tòa nhà
Ta có: \(\tan {24^ \circ } = \frac{{BH}}{{AH}} \Rightarrow BH = 30.\tan {24^ \circ } \approx 13,357\)
\( \Rightarrow BC = HC -HB \approx 1,5 + 18,5 - 13,357= 6,643(m)\)
Đúng 0
Bình luận (0)
Dynano là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynano làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diễn nào của anh chàng trẻ tuổi tài cao này khiến người xem kinh ngạc vì nó vượt qua giới hạn khoa học. Một lần đến NewYork anh ngẫu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di chuyển từ tòa nhà này đến tòa nhà khác và trong quá trình di chuyển đó có một lần anh đáp đất tại một điểm trong khoảng cách giữa hai tòa nhà (biết m...
Đọc tiếp
Dynano là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynano làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diễn nào của anh chàng trẻ tuổi tài cao này khiến người xem kinh ngạc vì nó vượt qua giới hạn khoa học. Một lần đến NewYork anh ngẫu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di chuyển từ tòa nhà này đến tòa nhà khác và trong quá trình di chuyển đó có một lần anh đáp đất tại một điểm trong khoảng cách giữa hai tòa nhà (biết mọi di chuyển của anh đều là đường thẳng). Biết tòa nhà ban đầu Dynano đứng có chiều cao là a(m), tòa nhà sau đó Dynano đến có chiều cao là b(m) (a < b) và khoảng cách giữa hai tòa nhà là c(m). Vị trí đáp đất cách tòa nhà thứ nhất là một đoạn là x(m). Hỏi x bằng bao nhiêu quãng đường di chuyển của Dynano là bé nhất?
A. x = 3 a c a + b .
B. x = a c 3 a + b .
C. x = a c a + b .
D. x = a c 2 a + b .
Đáp án C.
Màn biểu diễn của Dynano được biểu diễn theo mô hình bên
Cách 1: Áp dụng kiến thức “Giá trị lớn nhất – Giá trị nhỏ nhất của hàm số”
Ta có A B = c , A C = a , A D = b , A M = x . Khi đó C M = A C 2 + A M 2 = x 2 + a 2
Và
M D = B M 2 + B D 2 = ( c − x ) 2 + b 2 = x 2 − 2 c x + b 2 + c 2
Như vậy quãng đường di chuyển của Dynano là
T = C M + M D = x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 ( 0 < x < c ) .
Xét hàm số x 2 + a 2 + x 2 − 2 c x + b 2 + c 2 trên ( 0 ; c ) .
Đạo hàm f ' ( x ) = x x 2 + a 2 + x − c x 2 − 2 c x + b 2 + c 2 = 0
⇔ x x 2 − 2 c x + b 2 + c 2 = ( c − x ) x 2 + a 2 ⇔ x 2 c − x 2 + b 2 = c − x 2 x 2 + a 2
⇔ x 2 b 2 = c - x 2 a 2 ⇔ b x = ( c − x ) a ⇔ x = a c a + b ∈ ( 0 ; c ) .
Lập bảng biến thiên tìm ta được f(x) đạt nhỏ nhất khi x = a c a + b .
Cách 2: Dùng kiến thức hình học
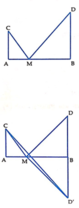
Gọi D' là điểm đối xứng với D qua AB. Khi đó M C + M D = M C + M D ' ≥ C D ' . Do vậy ( M C + M D ) min = C D ' . Dấu = xảy ra khi M ∈ C D ' hay M = C D ' ∩ A B .
Khi đó Δ A M C ∽ △ B M D '
⇒ A M B M = A C B D ' ⇔ x c − x = a b ⇔ x = a c a + b
Đúng 0
Bình luận (0)
Dynano là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynano làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diễn nào của anh chàng trẻ tuổi tài cao này khiến người xem kinh ngạc vì nó vượt qua giới hạn khoa học. Một lần đến NewYork anh ngẫu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di chuyển từ tòa nhà này đến tòa nhà khác và trong quá trình di chuyển đó có một lần anh đáp đất tại một điểm trong khoảng cách giữa hai tòa nhà (biết m...
Đọc tiếp
Dynano là một nhà ảo thuật gia đại tài người Anh nhưng người ta thường nói Dynano làm ma thuật chứ không phải làm ảo thuật. Bất kì màn trình diễn nào của anh chàng trẻ tuổi tài cao này khiến người xem kinh ngạc vì nó vượt qua giới hạn khoa học. Một lần đến NewYork anh ngẫu hứng trình diễn khả năng bay lơ lửng trong không trung của mình bằng cách di chuyển từ tòa nhà này đến tòa nhà khác và trong quá trình di chuyển đó có một lần anh đáp đất tại một điểm trong khoảng cách giữa hai tòa nhà (biết mọi di chuyển của anh đều là đường thẳng). Biết tòa nhà ban đầu Dynano đứng có chiều cao là a(m), tòa nhà sau đó Dynano đến có chiều cao là b(m) (a < b) và khoảng cách giữa hai tòa nhà là c(m). Vị trí đáp đất cách tòa nhà thứ nhất là một đoạn là x(m). Hỏi x bằng bao nhiêu quãng đường di chuyển của Dynano là bé nhất?
A. x = 3 a c a + b .
B. x = a c 3 a + b .
C. x = a c a + b .
D. x = a c 2 a + b .
Câu 3. Hai người đứng ở vị trí A và B quan sát một máy bay trực thăng đang ở vị trí C với các góc lần lượt là 45° và 30° (như hình vẽ (bên dưới). Biết máy bay cách vị trí B là 260m. tính khoảng cách từ máy bay đến vị trị A 45 ° 30 ° C A B Câu 4. Cho đường tròn (O) đường kính AB 2R. Trên đường tròn (O) lấy điểm C (C khác A, khác B) sao cho CA CB. Tiếp tuyến tại A của đường tròn (O) cắt BC tại Ea) Chứng minh tam giác ABC vuông và BC.BE4R2b) Đường thẳng qua A vuông góc với OE tạ...
Đọc tiếp
Câu 3. Hai người đứng ở vị trí A và B quan sát một máy bay trực thăng đang ở vị trí C với các góc lần lượt là 45° và 30° (như hình vẽ (bên dưới). Biết máy bay cách vị trí B là 260m. tính khoảng cách từ máy bay đến vị trị A
Câu 4. Cho đường tròn (O) đường kính AB = 2R. Trên đường tròn (O) lấy điểm C (C khác A, khác B) sao cho CA < CB. Tiếp tuyến tại A của đường tròn (O) cắt BC tại E
a) Chứng minh tam giác ABC vuông và BC.BE=4R2
b) Đường thẳng qua A vuông góc với OE tại I và cắt đường tròn (O) tại D. Chứng minh bồn điểm A, E,C,I cùng thuộc một đường tròn.
c) Chứng minh ED là tiếp tuyến của đường tròn (O) và góc ECD = góc EDB
Câu 3:
Xét ΔCAB có \(\dfrac{CB}{sinA}=\dfrac{CA}{sinB}\)
=>\(\dfrac{260}{sin45}=\dfrac{CA}{sin30}\)
=>\(CA\simeq183,85\left(m\right)\)
Câu 4:
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>AC\(\perp\)CB tại C
=>AC\(\perp\)EB tại C
Xét ΔABE vuông tại A có AC là đường cao
nên \(BC\cdot BE=BA^2=\left(2R\right)^2=4R^2\)
b: Ta có: ΔOAD cân tại O
mà OE là đường cao
nên OE là phân giác của góc AOD
Xét ΔOAE và ΔODE có
OA=OD
\(\widehat{AOE}=\widehat{DOE}\)
OE chung
Do đó: ΔOAE=ΔODE
=>\(\widehat{OAE}=\widehat{ODE}=90^0\)
Xét tứ giác EAOD có
\(\widehat{EAO}+\widehat{EDO}=90^0+90^0=180^0\)
=>EAOD là tứ giác nội tiếp
=>E,A,O,D cùng thuộc một đường tròn
c: Xét (O) có
OD là bán kính
ED\(\perp\)DO tại D
Do đó: ED là tiếp tuyến của (O)
Xét (O) có
\(\widehat{EDC}\) là góc tạo bởi tiếp tuyến DE và dây cung DC
\(\widehat{CBD}\) là góc nội tiếp chắn cung DC
Do đó: \(\widehat{EDC}=\widehat{CBD}\)
=>\(\widehat{EDC}=\widehat{EBD}\)
Xét ΔEDC và ΔEBD có
\(\widehat{EDC}=\widehat{EBD}\)
\(\widehat{DEC}\) chung
Do đó: ΔEDC đồng dạng với ΔEBD
=>\(\widehat{ECD}=\widehat{EDB}\)
Đúng 0
Bình luận (0)
1. Công viên giҧi trí có một bộ sưu tập mô hình các toà nhà và những điểm tham quan khắp thành phố với tỉ lệ 1:20. Tòa nhà United States Capitol cao 289 feet. Hỏi chiều cao của mô hình tòa nhà này trong công viên theo đơn vị feet là bao nhiêu? Làm tròn tới số nguyên gần nhất.
Chiều cao mô hình toà nhà:
289 : 20 = 14,45(ft)
Đúng 0
Bình luận (0)