hai đường chéo ABCD có cạch AB= 5 cm; hai đường chéo AC=8 cm và BD= 6 cm
a) tính chu vi của hình thoi ABCD
b) tính diện tích của hình thoi ABCD
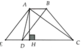
cho hình thang cân abcd có ab//dc và ab<dc, đường chéo bd vuông góc với cạch bên bc. vẽ đường cao bh,ak
a, cm tam giác bdc đồng dạng tam giác hbc
b, cm bc^2=hc.dc
c,cm tam giác akd đồng dạng tam giác bhc
d, cho bc=15cm. dc=25cm. tính hc,hd
e, tính diện tích hình thang abcd
a) Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
\(\widehat{HCB}\) chung
Do đó: ΔBDC\(\sim\)ΔHBC(g-g)
trong hình thoi abcd
cạnh ab =
cạch ad song song với cạnh ....
hình thoi abcd có độ dài hai đường chéo ac = 4cm db = 6cm diện tích hình thoi abcd là ..... cm2
Canh ab = bc canh ad song song voi canh bc dien h : 24 cm2
Cho hình thang ABCD (AB // CD) có hai đường chéo vuông góc với nhau. Đường cao là 12 cm, đường chéo BD là 15 cm. Tính diện tích hình thang ABCD.
Cho hình thang ABCD có hai đáy AB = 5cm, CD = 15 cm và hai đường chéo là AC = 16 cm, BD = 12 cm. Tính diện tích hình thang ABCD
Qua A kẻ AE//BD (E Î DC)
Þ AE = BD = 12cm, DE = AB = 5cm
Þ DAEC vuông tại A (định lý Pytago đảo)
⇒ A H = A E . A C E C = 12.16 20 = 9 , 6 c m
Þ SABCD = 96cm2
Cho hình thang ABCD có đáy bé AB=30 cm; đáy lớn CD=45 cm. Hai đường chéo cắt nhau tại O . Tính S\(_{ABCD}\) biết S\(_{AOB}\) =180 cm\(^2\)
Ta có :
Sdgc = 2/3 Sagc(vì có chung chiều cao và CD = 2/3 AC)Tỉ số giữa hai diện tích hay bằng tỉ số giữa 2 chiều cao.
Sagc = 400 : 2/3 = 600 (cm2)
Mà Scgb = 1/2 Sagc(vì có chung đáy CG và có chiều cao hạ từ B xuống CG bằng 1/2 chiều cao hạ từ A xuống.
Vậy Scgb = 600 x 1/2 = 300 (cm2)
Cho hình thoi ABCD, biết AB = 5 cm, AI = 3 cm ( I là giao điểm của hai đường chéo). Hãy tính diện tích hình thoi
Áp dụng Pi-ta-go vào tam giác vuông IAB, ta có: \(AB^2=AI^2+IB^2\)
\(\Rightarrow IB^2=AB^2-AI^2=25-9=16cm\)
\(\Rightarrow IB=4\left(cm\right)\)
\(AC=2AI=2.3=6\left(cm\right)\)
\(BD=2IB=2.4=8\left(cm\right)\)
\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.6.8=24\left(cm^2\right)\)
Chúc bạn học tốt !!!
Cho tứ giác ABCD có AB = 3 cm, BC = 10 cm, CD = 12 cm, AD = 5 cm, đường chéo BD = 6 cm.
Chứng minh:
a. ΔABD ∼ ΔBDC b. Tứ giác ABCD là hình thang
a: Xét ΔABD và ΔBDC có
AB/BD=BD/DC=AD/BC
Do đó: ΔABD∼ΔBDC
b: Ta có: ΔABD=ΔBDC
nên \(\widehat{ABD}=\widehat{BDC}\)
hay AB//CD
=>ABCD là hình thang
a, Ta có:\(\dfrac{AB}{BD}=\dfrac{3}{6}=\dfrac{1}{2}\\ \dfrac{BD}{DC}=\dfrac{6}{12}=\dfrac{1}{2}\\ \dfrac{AD}{BC}=\dfrac{5}{10}=\dfrac{1}{2}\\ \Rightarrow\dfrac{AB}{BD}=\dfrac{BD}{DC}=\dfrac{AD}{BC}=\dfrac{1}{2}\)
Xét ΔABD và ΔBDC có:
\(\dfrac{AB}{BD}=\dfrac{BD}{DC}=\dfrac{AD}{BC}\left(cmt\right)\)
\(\Rightarrow\Delta ABD\sim\Delta BDC\left(c.c.c\right)\)
b, Ta có \(\Delta ABD\sim\Delta BDC\left(cma\right)\Rightarrow\widehat{ABD}=\widehat{BDC}\)
Mà 2 góc này là 2 góc so le trong \(\Rightarrow AB//CD\)
\(\Rightarrow\)Tứ giác ABCD là hình thang
Cho hình thoi ABCD biết độ dài hai đường chéo lần lượt là 6 cm và 8 cm giao điểm của hai đường chéo là H. a Tính độ dài đoạn AB. b. Tính khoảng cách từ điểm H đến AB.
Cho hình thang ABCD có , hai đường chéo vuông góc với nhau tại H.
Biết AB = 3căn 5 ,HA=3. Khi đó độ dài HC là cm.
Cho hình thang ABCD có góc B= góc C =90o. Hai đường chéo vuông góc với nhau tại H. Biết AB=3 căn 5 cm,HA=3cm.Tinh HB,HC,HD