So sánh các cạnh của tam giác ABC biết A) góc ngoài của đỉnh góc A =120° ; góc B = 50° B) tam giác ABC cân tại A ,A>60° C) A=40° và số đo góc B và C tỉ lệ với 3 ; 4
DT
Những câu hỏi liên quan
Cho tam giác ABC có góc ngoài tại đỉnh A là 120 độ , góc B bằng 70 ,độ kẻ phân giác BE
a ,Tính góc AEB
b, so sánh các cạnh của tam giác ABE
c, So sánh các cạnh của tam giác Bec
a: góc BAC=180-120=60 độ
góc ABE=70/2=35 độ
góc AEB=180-60-35=85 độ
b: góc ABE<góc BAE<góc AEB
=>AE<BE<AB
c: góc ECB=180-70-60=50 độ
góc BEC=180-85=95 độ
Vì góc EBC<góc ECB<góc BEC
nên EC<EB<BC
Đúng 1
Bình luận (0)
Cho tam giác ABC và biết góc A + C = 120 độ, góc A - C = 40 độ
a) So sánh các cạnh của tam giác ABC.
b) Tia phân giác của góc A cắt BC ở D. So sánh độ dài các đoạn BD và CD.
Cho tam giác ABC có AB < AC, tia phân giác của góc A cắt BC tại D. Trên cạnh AC lấy điểm E sao cho AB=AE
. So sánh góc (DEC) và góc ngoài tại đỉnh B của tam giác ABC
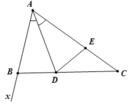
b. Giả sử góc ngoài tại đỉnh B của tam giác ABC là ∠(xBC). Ta có:
∠(xBC) + ∠(ABD) = 180o ⇒ ∠(xBC) = 180o - ∠(ABD) (0.5 điểm)
∠(DEC) + ∠(AED) = 180o ⇒ ∠(DEC) = 180o - ∠(AED) (0.5 điểm)
Mà ∠(ABD) = ∠(AED) ( hai góc tương ứng vì ΔABD = ΔAED)(0.5 điểm)
Từ đó suy ra ∠(xBC) = ∠(DEC) (0.5 điểm)
Đúng 0
Bình luận (0)
Cho tam giác ABC, biết góc A+ góc B=120, góc A- góc B=30.
a) So sánh các cạnh của tam giác.
b) Tia p/giáp góc A cắt BC ở D. So sánh độ dài các đoạn BD và CD( vẽ hình)
Cho tam giác ABC , biết góc A + góc B = 120 độ , góc A - góc B = 30 độ
A) So sánh các cạnh của tam giác
B) Tia phân giác của góc A cắt BC tại D . So sánh độ dài DB và CD
Ta có :
A + B = 120 (1)
A - B = 30 => A = 30 + B (2)
Thay (2) vào (1) , ta có :
30 + B + B = 120
30 + 2B = 120
2B = 90
=> B = 45
Thay B vào lại (1) ,ta có :
A + B = 120
=> A + 45 = 120
=> A = 75
Áp dụng tổng 3 góc trong một tam giác ,ta có :
A + B + C = 180
75 + 45 + C = 180
=> C = 60
Vậy A = 75
B = 45
C = 60
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 5cm AC = 3 cm
a) So sánh góc B với góc C
b) So sánh 2 góc ngoài tại đỉnh B và C của tam giác ABC
a: Xét ΔABC có AB>AC
nên \(\widehat{B}< \widehat{C}\)
b: Vì \(\widehat{B}< \widehat{C}\)
nên góc ngoài tại đỉnh B lớn hơn góc ngoài tại đỉnhC
Đúng 1
Bình luận (0)
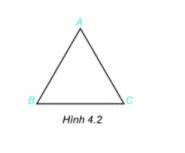
Cho tam giác đều ABC như hình 4.2.
1. Gọi tên các đỉnh, cạnh góc của tam giác đều ABC.
2. Dùng thước thẳng để đo và so sánh các cạnh của tam giác ABC.
3. Sử dụng thước đo góc để đo và so sánh các góc của tam giác ABC.
1) Các đỉnh : A, B, C
Các cạnh: AB, BC, AC
Các góc: \(\widehat A,\,\widehat B,\,\widehat C\)
2) AB =3 cm, AC = 3 cm, BC = 3 cm nên các cạnh của tam giác ABC bằng nhau
3) \(\widehat A = 60^0; \widehat B =60^0; \widehat C=60^0\) nên các góc của tam giác ABC bằng nhau và bằng 60o
Đúng 1
Bình luận (0)
Cho tam giác ABC góc A bằng 120 độ các tia phân giác của góc A và C cắt nhau ở O, cắt các cạnh BC và AB lần lượt ở D và E. Đường phân giác góc ngoài tại đỉnh B của tam giác ABC cắt đường thẳng AC tại F. Chứng minh a,BO vuông góc với BF b, góc BDF bằng góc ADF c, 3 điểm D, E, F thẳng hàng
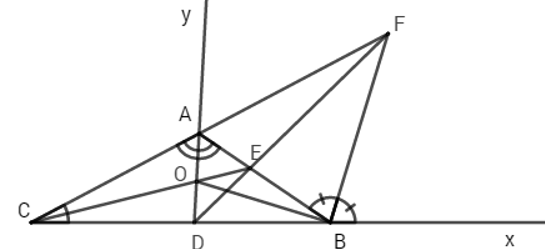
a) Xét \(\Delta ABC\) có tia phân giác \(BAC,ACB\) cắt nhau tại O suy ra O là giao điểm của 3 đường phân giác trong tam giác ABC suy ra BO là phân giác của \(\widehat{CBA}\) (tính chất 3 đường phân giác của tam giác)
\(\Rightarrow DBO=ABO=\dfrac{DBA}{2}\left(1\right)\) ( tính chất tia phân giác )
Lại có BF là phân giác của \(\widehat{ABx\left(gt\right)}\) \(=ABF=FBx\left(2\right)\)
( tính chất của tia phân giác )
Mà \(ABD+ABx=180^o\left(3\right)\left(kềbu\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow OBA+ABF=180^o\div2=90^o\Rightarrow BO\text{⊥ }BF\)
b) Ta có \(FAB+BAC=180^o\)( kề bù ) mà \(BAC=120^o\left(gt\right)\Rightarrow FAB=60^o\)
\(\Rightarrow\text{AD là phân giác của}\widehat{BAC}\) ( dấu hiệu nhận biết tia phân giác )
\(\Rightarrow BAD=CAD=60^o\) ( tính chất tia phân giác )
\(\Rightarrow FAy=CAD=60^o\) ( đối đỉnh ) \(\Rightarrow FAB=FAy=60^o\Rightarrow\) AF là tia phân giác của \(BAy\) ( dấu hiệu nhận biết tia phân giác )
Vậy \(\Delta ABD\) có hai tia phân giác của hai góc ngoài tại đỉnh A và đỉnh B cắt nhau tại F nên suy ra DF là phân giác của \(ADB=BDF=ADF\) ( tính chất tia phân giác )
c) Xét \(\Delta ACD\) có phân giác góc ngoài tại đỉnh A và phân giác trong tại đỉnh C cắt nhau tại E nên suy ra DE cũng là phân giác của \(ADB\Rightarrow\)\(D,E,F\) thẳng hàng
Đúng 6
Bình luận (1)
Cho tam giác ABC có góc ngoài đỉnh C bằng 120 độ ,A -B =60 độ .Tính các góc của tam giác ABC
Iu mn nhìu !
Vì góc ngoài đỉnh C bằng 120 độ nên \(\widehat{A}+\widehat{B}=120^0\)
Mà \(\widehat{A}-\widehat{B}=60^0\Rightarrow\left\{{}\begin{matrix}\widehat{A}=\left(120^0+60^0\right):2=90^0\\\widehat{B}=120^0-90^0=30^0\end{matrix}\right.\)
\(\Rightarrow\widehat{C}=180^0-90^0-30^0=60^0\)
Đúng 1
Bình luận (1)




