cho 2 đường thẳng d1: x + 2y + 4 = 0; d2: 2x - y + 6 = 0. Số đo góc giữa d1; d2 là:
A. 300
B. 600
C. 450
D. 900
Cho ba đường thẳng d 1 : x − 2 y + 1 = 0 , d 2 : m x − 3 m − 2 y + 2 m − 2 = 0 , d 3 : x + y − 5 = 0 . Giá trị m để hai đường thẳng d1;d2 cắt nhau tại một điểm nằm trên d3 là
A.m = 0
B.m = 1
C.m = 2
D. không tồn tại m thỏa mãn
Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D
Cho đường tròn tiếp xúc với cả đường thẳng d1: x+2y-4=0, d2: x+2y+6=0. Khi đó diện tích hình tròn là
A. 5π
B. 10π
C. 20π
D. 40π
Ta có: 1 1 = 2 2 ≠ − 4 6
Suy ra: d1 // d2.
Do đó, đường tròn tiếp xúc với cả hai đường thẳng song song thì khoảng cách hai đường thẳng đó bằng đường kính của đường tròn.
* Tính khoảng cách 2 đường thẳng :

Đáp án A
Cho 2 đường thẳng (d1) y=3x + 4 và (d2) x - 2y =0 một điểm A ( -1; 1)
a xét vị trí tương đối của A với 2 đường thẳng
b tìm giao điểm (d1) và ( d2)
c tìm m để (d3) : ( m-1)x + (m-2)y + m +1=0 đồng quy với (d1) và (d2)
a) Thay hoành độ và tung độ của A vào 2 pt đường thẳng (d1) và (d2), ta lần lượt được:
\(1=3\left(-1\right)+4\) (luôn đúng)
\(-1-2.1=0\) (vô lí)
Như vậy, \(A\in d_1;A\notin d_2\)
b) Gọi giao điểm của d1, d2 là \(B\left(x_0;y_0\right)\). Khi đó \(x_0,y_0\) là các số thỏa mãn \(\left\{{}\begin{matrix}y_0=3x_0+4\\x_0-2y_0=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=6y_0+4\\x_0=2y_0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=-\dfrac{4}{5}\\x_0=-\dfrac{8}{5}\end{matrix}\right.\)
Vậy giao điểm của d1 và d2 là \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
c) Để đường thẳng d1, d2, d3 đồng quy thì d3 phải đi qua giao điểm của d1 và d2. Nói cách khác, d3 phải đi qua điểm \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
\(\Leftrightarrow\left(m-1\right).\dfrac{-8}{5}+\left(m-2\right).\dfrac{-4}{5}+m+1=0\)
\(\Leftrightarrow\dfrac{21}{5}-\dfrac{7}{5}m=0\)
\(\Leftrightarrow m=3\)
Vậy \(m=3\) thỏa mãn ycbt.
Cho đường thẳng d1:x+2y-3=0 ; d2:x+2y-5=0 và A(1,3). Viết phương trình đường thẳng qua A và cắt d1,d2 lần lượt tại B,C sao cho SABC=5/4, với O là gốc tọa độ
Trong không gian Oxyz cho 2 đường thẳng d 1 : x + 3 2 = y + 2 - 1 = z + 2 - 4 ; d 2 : x + 1 3 = y + 1 2 = z - 2 3 và mặt phẳng ( P ) : x + 2 y + 3 z - 7 = 0 Đường thẳng vuông góc với mặt phẳng (P), cắt d 1 và d 2 có phương trình là:

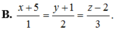
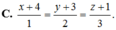
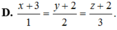
Đáp án B.
Gọi ![]()
thuộc
d
1
và ![]()
thuộc d 2 là 2 giao điểm.
Ta có: ![]()
Vì M N → cùng phương với
![]() nên ta có:
nên ta có:
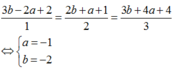
![]() điểm này thuộc đường thẳng ở đáp án B.
điểm này thuộc đường thẳng ở đáp án B.
Cho hai đường thẳng d1 : x+ 2y -1 = 0 và d2 : x- 3y +3 = 0. Phương trình đường thẳng d đối xứng với d1 qua là: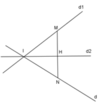
A. x -3y- 2= 0
B.x+ 3y+1= 0
C. 3x-y=1= 0
D. x-3y+ 3=0
Đáp án D
Gọi I là giao điểm của hai đường thẳng d1; d2 . Tọa độ điểm I là nghiệm của hệ:
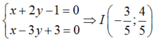
Lấy điểm m 1 ; 0 ∈ d 1 . Đường thẳng qua M và vuông góc với d2 có phương trình: 3x + y-3= 0
Gọi H = ∆ ∩ d 2 suy ra tọa độ điểm H là nghiệm của hệ:
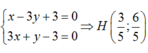
Phương trình đường thẳng
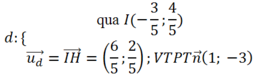
có dạng:
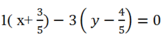
hay x-3y + 3= 0
Cho đường thẳng d1: 2x+y-2=0 và đường thẳng d2: x-y+2=0 và d3: x+2y+3=0. Tìm điểm M thuộc d1 cách đều d2 và d3
Trong không gian Oxyz, cho mặt phẳng (P):x+2y+3z-7=0 và hai đường thẳng d 1 : x + 3 2 = y + 2 - 1 = z + 2 - 4 ; d 2 : x + 1 3 = y + 1 2 = z - 2 3 Đường thẳng vuông góc với mặt phẳng (P) và cắt cả hai đường thẳng d1 và d2 có phương trình là
A. x + 7 1 = y 2 = z - 6 3
B. x + 5 1 = y + 1 2 = z - 2 3
C. x + 4 1 = y + 3 2 = z + 1 3
D. x + 3 1 = y + 2 2 = z + 2 3
Trong không gian Oxyz cho 2 đường thẳng
d 1 : x + 3 2 = y + 2 − 1 = z + 2 − 4 , d 2 : x + 1 3 = y + 1 2 = z − 2 3 và mặt phẳng P : x + 2 y + 3 z − 7 = 0. Đường thẳng vuông góc với mặt phẳng (P), cắt d 1 và d 2 có phương trình là
A. x + 7 1 = y 2 = z − 6 3 .
B. x + 5 1 = y + 1 2 = z − 2 3 .
C. x + 4 1 = y + 3 2 = z + 1 3 .
D. x + 3 1 = y + 2 2 = z + 2 3 .
Đáp án B.
Gọi M 2 a − 3 ; − 2 − a ; − 2 − 4 a thuộc d 1 và N − 1 + 3 b ; − 1 + 2 b ; 2 + 3 b thuộc d 2 là 2 giao điểm.
Ta có:
M N → = 3 b − 2 a + 2 ; 2 b + a + 1 ; 3 b + 4 a + a .
Vì M N → cùng phương với n P → = 1 ; 2 ; 3 nên ta có:
3 b − 2 a + 2 1 = 2 b + a + 1 2 = 3 b + 4 a + 4 3 ⇔ a = − 1 b = − 2
⇒ M − 5 ; − 1 ; 2 , điểm này thuộc đường thẳng ở đáp án B.