Với vectơ bất kì \(\overrightarrow{a}\) và mọi số thực k,l; chứng minh:
\(k\left(l.\overrightarrow{a}\right)=l\left(k.\overrightarrow{a}\right)\)
Gấp nha:(((
@Nguyễn Việt Lâm @Akai Haruma
Chứng minh khẳng định sau: Hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương khi và chỉ khi có một số thực k sao cho \({x_1}{\rm{ = }}k{x_2}\) và \({y_1} = {\rm{ }}k{y_2}\).
Để hai vectơ \(\overrightarrow u = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v = \left( {{x_2},{y_2}} \right)\) (\(\overrightarrow v \ne 0\) ) cùng phương thì phải tồn tại một số \(k\left( {k \in \mathbb{R}} \right)\) sao cho \(\overrightarrow u = k.\overrightarrow v \Leftrightarrow \left\{ \begin{array}{l}{x_1} = k{x_2}\\{y_1} = k{y_2}\end{array} \right.\) ( ĐPCM)
Cho tam giác ABC với I, J lần lượt là trung điểm Của CB, CA đồng thời G là trọng tâm
a) Hãy biểu diễn \(\overrightarrow{IJ}\) theo \(\overrightarrow{BA}\)
b) CMR: với mọi điểm M bất kì ta luôn có \(\overrightarrow{MB}+\overrightarrow{MC}=2\overrightarrow{MI}\)
c) CMR: với mọi điểm M bất kì ta luôn có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MG}\)
Chứng minh rằng với hai vecto bất kì \(\overrightarrow a ,\overrightarrow b \), ta có:
\(\begin{array}{l}{(\overrightarrow a + \overrightarrow b )^2} = {\overrightarrow a ^2} + 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}\\{(\overrightarrow a - \overrightarrow b )^2} = {\overrightarrow a ^2} - 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}\\(\overrightarrow a - \overrightarrow b )(\overrightarrow a + \overrightarrow b ) = {\overrightarrow a ^2} - {\overrightarrow b ^2}\end{array}\)
\(\begin{array}{l}{ + \, (\overrightarrow a + \overrightarrow b )^2} = (\overrightarrow a + \overrightarrow b )(\overrightarrow a + \overrightarrow b )\\ = \overrightarrow a .(\overrightarrow a + \overrightarrow b ) + \overrightarrow b .(\overrightarrow a + \overrightarrow b ) \\= {\overrightarrow a ^2} + \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow a + {\overrightarrow b ^2} \\= {\overrightarrow a ^2} + 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}.\\ + \, {(\overrightarrow a - \overrightarrow b )^2} =(\overrightarrow a - \overrightarrow b )(\overrightarrow a - \overrightarrow b )\\ = \overrightarrow a .(\overrightarrow a - \overrightarrow b ) - \overrightarrow b .(\overrightarrow a - \overrightarrow b ) \\= {\overrightarrow a ^2} - \overrightarrow a .\overrightarrow b - \overrightarrow b .\overrightarrow a + {\overrightarrow b ^2} \\= {\overrightarrow a ^2} - 2\overrightarrow a .\overrightarrow b + {\overrightarrow b ^2}. \\ + \, (\overrightarrow a - \overrightarrow b )(\overrightarrow a + \overrightarrow b ) \\= \overrightarrow a .(\overrightarrow a - \overrightarrow b ) + \overrightarrow b .(\overrightarrow a - \overrightarrow b ) \\= {\overrightarrow a ^2} - \overrightarrow a .\overrightarrow b + \overrightarrow b .\overrightarrow a - {\overrightarrow b ^2} \\= {\overrightarrow a ^2} - {\overrightarrow b ^2}.\end{array}\)
Với mọi số thực dương a và m, n là hai số thực bất kì. Mệnh đề nào dưới đây đúng?
A. a m n = a m + n
B. a m a n = a m − n
C. a m n = a m n
D. a m a n = a n − m
Phương pháp:
Sử dụng các công thức của lũy thừa và chọn đáp án đúng.
Cách giải:
Với hai vectơ \(\overrightarrow a ,\overrightarrow b \) cho trước, lấy một điểm A vẽ các vectơ \(\overrightarrow {AB} = \overrightarrow a ,\;\overrightarrow {BC} = \overrightarrow b \). Lấy điểm A’ khác A và cũng vẽ các vectơ \(\overrightarrow {A'B'} = \overrightarrow a ,\;\overrightarrow {B'C'} = \overrightarrow b \). Hỏi hai vectơ \(\overrightarrow {AC} \) và \(\overrightarrow {A'C'} \) có mối quan hệ gì?
\(\overrightarrow {AB} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}AB//\;a\\AB = a\end{array} \right.\) và \(\overrightarrow {A'B'} = \overrightarrow a \;\;\, \Rightarrow \left\{ \begin{array}{l}A'B'\;//\;a\\A'B' = a\end{array} \right.\)
\( \Rightarrow \left\{ \begin{array}{l}AB//\;A'B'\\AB = A'B'\end{array} \right.\)
Tương tự, ta cũng suy ra \(\left\{ \begin{array}{l}BC//\;B'C'\\BC = B'C'\end{array} \right.\)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c-g-c)
\(\left\{ \begin{array}{l}AC//\;A'C'\\AC = A'C'\end{array} \right.\)
Dễ dàng suy ra \(\overrightarrow {AC} = \overrightarrow {A'C'} \).
Cho hình lăng trị tứ giác ABC.A'B'C'D'. Mặt phẳng (P) cắt các cạnh bên AA', BB',CC', DD' lần lượt tại I, K, L, M. Xét các vectơ có các điểm đầu là các điểm I, K, L, M và có các điểm cuối là các đỉnh của lăng trụ. Hãy chỉ ra các vectơ :
a) Cùng phương với \(\overrightarrow{IA}\)
b) Cùng hướng với \(\overrightarrow{IA}\)
c) Ngược hướng với \(\overrightarrow{IA}\)
a) Các véctơ cùng phương với là:
,
,
,
,
,
,
.
b) Các véctơ cùng hướng với là:
,
,
.
c) Các véctơ ngược hướng với là:
,
,
,
.
Trong mặt phẳng Oxy, cho hai vectơ \(\overrightarrow a = \left( {{a_1},{a_2}} \right),\overrightarrow b = \left( {{b_1},{b_2}} \right)\) và số thực k. Ta đã biết có thể biểu diễn từng vectơ \(\overrightarrow a ,\overrightarrow b \) theo hai vectơ , \(\overrightarrow j \) như sau
a) Biểu diễn từng vectơ \(\overrightarrow a + \overrightarrow b ,\overrightarrow a - \overrightarrow b ,k\overrightarrow a \) theo hai vectơ , \(\overrightarrow j \)
b) Tìm \(\overrightarrow a .\overrightarrow b \) theo tọa độ của hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \)
a) Ta có
\(\begin{array}{*{20}{l}}
{\vec a + \vec b = \left( {{a_1} + {a_2}\vec j} \right) + \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} + {b_1}} \right) + \left( {{a_2} + {b_2}} \right)}\\
{\vec a - \vec b = \left( {{a_1} + {a_2}\vec j} \right) - \left( {{b_1} + {b_2}\vec j} \right) = \left( {{a_1} - {b_1}} \right) + \left( {{a_2} - {b_2}} \right)}\\
{k\vec a = k\left( {{a_1} + {a_2}\vec j} \right) = k{a_1} + k{a_2}\vec j}
\end{array}\)
b) Ta có
\(\begin{array}{l}
\vec a.\vec b = \left( {{a_1}\overrightarrow i + {a_2}\vec j} \right).\left( {{b_1}\overrightarrow i + {b_2}\vec j} \right)\\
= {a_1}{b_1}{\overrightarrow i ^2} + {a_1}{b_2}\overrightarrow i .\vec j + {a_2}{b_1}\overrightarrow i \vec j + {a_2}{b_2}{{\vec j}^2}\\
= {a_1}{b_1} + {a_2}{b_2}
\end{array}\)
Vì \({\overrightarrow i ^2} = {\left| {\overrightarrow i } \right|^2} = 1,{\overrightarrow j ^2} = {\left| {\overrightarrow j } \right|^2} = 1,\overrightarrow i \overrightarrow j = 0\)
Cho ba vectơ \(\overrightarrow a ,\;\overrightarrow b ,\;\overrightarrow u \) với \(|\overrightarrow a |\; = \;\,|\overrightarrow b |\; = 1\) và \(\overrightarrow a \bot \overrightarrow b \). Xét một hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b .\) Chứng minh rằng:
a) Vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
b) \(\overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \)
Tham khảo:
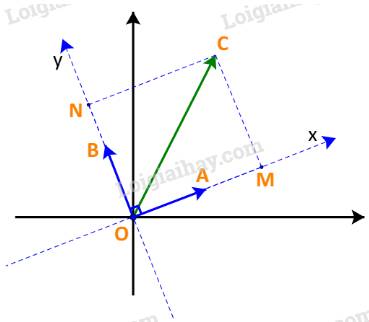
a) Trên mặt phẳng tọa độ, lấy các điểm A, B, C sao cho \(\overrightarrow {OA} = \overrightarrow a ;\;\overrightarrow {OB} = \overrightarrow b ;\;\overrightarrow {OC} = \overrightarrow u \)
Trên hệ trục Oxy với các vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), lấy M, N là hình chiếu của C trên Ox, Oy.
Gọi tọa độ của \(\overrightarrow u \)là \(\left( {x;y} \right)\). Đặt \(\alpha = \left( {\overrightarrow u ,\overrightarrow a } \right)\).
+) Nếu \({0^o} < \alpha < {90^o}\): \(x = OM = \;|\overrightarrow u |.\cos \alpha = \;|\overrightarrow u |.\cos \alpha .\;|\overrightarrow a |\; = \overrightarrow u \,.\,\overrightarrow a \,;\)
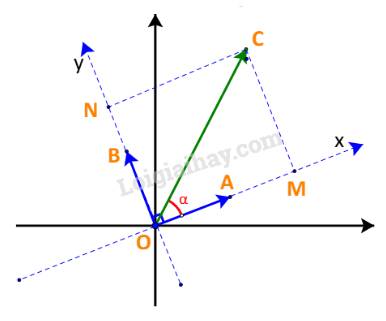
+) Nếu \({90^o} < \alpha < {180^o}\): \(x = - OM = \; - |\overrightarrow u |.\cos ({180^o} - \alpha ) = \;|\overrightarrow u |.\cos \alpha \; = \overrightarrow u \,.\,\overrightarrow a \,;\)

Như vậy ta luôn có: \(x = \overrightarrow u .\overrightarrow a \)
Chứng minh tương tự, ta có: \(y = \overrightarrow u .\overrightarrow b \)
Vậy vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
b) Trong hệ trục Oxy với các vectơ vectơ đơn vị \(\overrightarrow i = \overrightarrow a ,\;\overrightarrow j = \overrightarrow b \), vectơ \(\overrightarrow u \) có tọa độ là \((\overrightarrow u \,.\,\overrightarrow a \,;\,\overrightarrow u \,.\,\overrightarrow b )\)
\(\begin{array}{l} \Rightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow i + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow j \\ \Leftrightarrow \overrightarrow u = (\overrightarrow u \,.\,\overrightarrow a \,).\overrightarrow a + (\,\overrightarrow u \,.\,\overrightarrow b ).\overrightarrow b \end{array}\)
Xét các vectơ cùng phương trong Hình 4.7. Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \)được gọi là cùng hướng, còn hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) được gọi là ngược hướng. Hãy chỉ ra các vectơ cùng hướng với vectơ \(\overrightarrow a \) và các vectơ ngược hướng với vectơ \(\overrightarrow a \).
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.