Bài 2 Cho hai đường thẳng AB và CD cắt nhau tại điểm O; biết góc AOC = góc 2BOD . Tính số đo của bốn góc tạo thành
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
CX
Những câu hỏi liên quan
Cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.
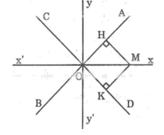
* Xét điểm M nằm trong góc AOD
Kẻ MH ⊥ OA, MK ⊥ OD
Xét hai tam giác MHO và MKO:
∠(MHO) = ∠(MKO) = 90o
MH = MK
OM cạnh huyền chung
Suy ra: ΔMHO = ΔMKO
(cạnh huyền - cạnh góc vuông)
Suy ra: ∠(MOH) = ∠(MOK)(2 góc tương ứng)
Hay OM là tia phân giác của ∠(AOD).
* Ngược lại, M nằm trên tia phân giác của ∠(AOD)
Xét hai tam giác vuông MHO và MKO, ta có:
∠(MHO) = ∠(MKO)= 90o
∠(MOH) = ∠(MOK)
OM cạnh huyền chung
Suy ra: ΔMHO = ΔMKO (cạnh huyền - góc nhọn)
Suy ra: MH = MK (2 cạnh tương ứng)
Vậy tập hợp các điểm M cách đều OA và OD là tia phân giác Ox của góc AOD.
Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.
Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.
Đúng 0
Bình luận (0)
1.Hai đường thẳng AB và CD cắt nhau tại O, tạo thành góc bằng 110º. Tính ba góc còn lại2. Hai đường thẳng AB và CD cắt nhau tại O. Biết – 20º. Tính mỗi góc , , , .3. Hai đường thẳng CD và EF cắt nhau tại O tạo thành bốn góc không có điểm trong chung. Biết tổng của ba trong bốn góc ấy bằng 300º. Tính số đo của bốn góc nói trên (cho biết )4. Hai đường thẳng AB và CD cắt nhau tại O tạo thành góc bằng 50º. Gọi OM là tia phân giác của góc , ON là tia đối của OM. Tính ,
Đọc tiếp
1.Hai đường thẳng AB và CD cắt nhau tại O, tạo thành góc bằng 110º. Tính ba góc còn lại
2. Hai đường thẳng AB và CD cắt nhau tại O. Biết –
= 20º. Tính mỗi góc
,
,
,
.
3. Hai đường thẳng CD và EF cắt nhau tại O tạo thành bốn góc không có điểm trong chung. Biết tổng của ba trong bốn góc ấy bằng 300º. Tính số đo của bốn góc nói trên (cho biết <
)
4. Hai đường thẳng AB và CD cắt nhau tại O tạo thành góc bằng 50º. Gọi OM là tia phân giác của góc
, ON là tia đối của OM. Tính
,
cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD.
Cho hai đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều hai đường thẳng AB và CD ?
Nếu điểm M nằm trong góc AOD thì kẻ MH vuông góc với OA, MK vuông góc với OD
Xét ΔMHO vuông tại H và ΔMKO vuông tại K có
MO chung
MH=MK
Do đó: ΔMHO=ΔMKO
Suy ra: \(\widehat{MOH}=\widehat{MOK}\)
=>M nằm trên tia phân giác của góc AOD
Vì ΔMHO=ΔMKO nên MH=MK
=>Tập hợp điểm M cách đều OA và OD là phân giác Ox của góc AOD
Tương tự M nằm trong các góc AOC, DOB, BOC thì tập hợp các điểm M là tia phân giác Oy, Oy’, Ox’.
Vậy tập hợp các điểm M cách đều hai đường thẳng AB và CD cắt nhau tại O là hai đường thẳng xx’ và yy’ là đường phân giác của các góc tạo bởi hai đường thẳng AB và CD.
Đúng 0
Bình luận (0)
Bài 7 (2) :Cho hình thang ABCD (AB//CD) ; hai đường chéo cắt nhau tại O. Qua O kẻ đường thẳng song song với AB cắt AD lần lượt tại M và N . Chứng minh OM = ON
HAI ĐƯỜNG THẲNG AB VÀ CD CẮT NHAU TẠI ĐIỂM O . CÁC GÓC KHÁC GÓC BẸT LÀ :............................
HAI ĐƯỜNG THẲNG AB VÀ XY CẮT NHAU TẠI ĐIỂM I . CÁC GÓC KHÁC GÓC BẸT LÀ:................................
Cho 2 đường thẳng AB và CD cắt nhau tại O. Tìm tập hợp các điểm cách đều 2 đường thẳng AB và CD
tập hợp các điểm cách đều 2 đường thẳng AB và CD
chỉ được 1 điểm
điểm giao điểm với 2 đt đó là O
Đúng 0
Bình luận (0)
Cho hai đường (O) và (O') cắt nhau ở hai điểm A và B. qua A vẽ hai đường thẳng (d) và (d'), đường thẳng (d) cắt (O) tại C và cắt (O') tại D, đường thẳng (d') cắt (O) tại M và cắt (O') tại N sao cho AB là phân giác của góc MAD. Cmr: CD=MN
Cho hai đường (O) và (O') cắt nhau ở hai điểm A và B. qua A vẽ hai đường thẳng (d) và (d'), đường thẳng (d) cắt (O) tại C và cắt (O') tại D, đường thẳng (d') cắt (O) tại M và cắt (O') tại N sao cho AB là phân giác của góc MAD. Cmr: CD=MN


