cho 2> a, b, c và a, b, c không âm; biết a+ b+ c= 3
CMR: a2+ b2+ c2 nhỏ hơn hơn hoặc bằng 5
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho a, b, c là các số không âm và không lớn hơn 2 thoả mãn \(a+b+c=3\). Chứng minh rằng: \(a^2+b^2+c^2\le5\).
Do \(0\le a;b;c\le2\)
\(\Rightarrow abc+\left(2-a\right)\left(2-b\right)\left(2-c\right)\ge0\)
\(\Leftrightarrow2\left(ab+bc+ca\right)-4\left(a+b+c\right)+8\ge0\)
\(\Leftrightarrow2\left(ab+bc+ca\right)\ge4\)
\(\Leftrightarrow\left(a+b+c\right)^2-\left(a^2+b^2+c^2\right)\ge4\)
\(\Leftrightarrow9-\left(a^2+b^2+c^2\right)\ge4\)
\(\Leftrightarrow a^2+b^2+c^2\le5\)
Dấu "=" xảy ra khi \(\left(a;b;c\right)=\left(0;1;2\right)\) và các hoán vị
cho a,b,c là các số không âm và không lớn hơn 2 thỏa mãn a+b+c=3.chứng minh :a*2+b*2+c*2<=5
Qúa dễ luôn
Ta có : a x 2 + b x 2 + c x 2 \(\le\) 5
2 x ( a + b + c ) \(\le\)5
a + b + c \(\le\) 5/2
a + b + c \(\le\) 2,5
Mà theo đề bài : a + b + c không lớn hơn 2 ( có nghĩa là bé hơn 2 ) . Nên a + b + c phải luôn luôn bé hơn 2,5 ( vì 2 luôn bé hơn 2,5 )
Vậy : a x 2 + b x 2 + c x 2 \(\le\) 5
cho a,b,c không âm và a+b+c=3. chứng minh rằng 1/a^2 +1/c^2 +1/b^2>= a^2+b^2+c^2
HELP ME!!!
\(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{1+1+1}{a^2+b^2+c^2}=\frac{3}{a^2+b^2+c^2}=\frac{a+b+c}{a^2+b^2+c^2}\)
Đề sai rùi bạn.
Phải là \(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\le a^2+b^2+c^2\)
Cho a;b;c là các số thực không âm thỏa mãn: \(a^2+b^2+c^2=3\)
Tìm min và max của \(A=a^3+b^3+c^3\)
\(a^3+a^3+1\ge3\sqrt[3]{a^3.a^3.1}=3a^2\)
Tương tự: \(2b^3+1\ge3b^2\) ; \(2c^3+1\ge3c^2\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)+3\ge3\left(a^2+b^2+c^2\right)=9\)
\(\Rightarrow a^3+b^3+c^3\ge3\)
\(A_{min}=3\) khi \(a=b=c=1\)
Lại có: \(\left\{{}\begin{matrix}a;b;c\ge0\\a^2+b^2+c^2=3\end{matrix}\right.\) \(\Rightarrow0\le a;b;c\le\sqrt{3}\)
\(\Rightarrow a^2\left(a-\sqrt{3}\right)\le0\Rightarrow a^3\le\sqrt{3}a^2\)
Tương tự: \(b^3\le\sqrt{3}b^2\) ; \(c^3\le\sqrt{3}c^2\)
\(\Rightarrow a^3+b^3+c^3\le\sqrt{3}\left(a^2+b^2+c^2\right)=3\sqrt{3}\)
\(A_{max}=3\sqrt{3}\) khi \(\left(a;b;c\right)=\left(0;0;\sqrt{3}\right)\) và các hoán vị
Tại điểm O trong môi trường đẳng hướng không hấp thụ âm và phản xạ âm, phát ra âm với công suất không đổi. Trên tia Ox theo thứ tự có ba điểm A, B, C sao cho OC = 4OA. Biết mức cường độ âm tại B là 2 B, tổng mức cường độ âm tại A và C là 4 B. Nếu AB = 20 m thì:
A BC=40 m
B. BC=80 m
C. BC=30 m
D. BC=20 m
Tại điểm O trong môi trường đẳng hướng không hấp thụ âm và phản xạ âm, phát ra âm với công suất không đổi. Trên tia Ox theo thứ tự có ba điểm A, B, C sao cho OC = 4OA. Biết mức cường độ âm tại B là 2 B, tổng mức cường độ âm tại A và C là 4 B. Nếu AB = 20 m thì
A. BC = 40 m.
B. BC = 80 m.
C. BC = 30 m.
D. BC = 20 m.
Tại điểm O trong môi trường đẳng hướng không hấp thụ âm và phản xạ âm, phát ra âm với công suất không đổi. Trên tia Ox theo thứ tự có ba điểm A, B, C sao cho OC = 4OA. Biết mức cường độ âm tại B là 2 B, tổng mức cường độ âm tại A và C là 4 B. Nếu AB = 20 m thì
A. BC = 40 m.
B. BC = 80 m.
C. BC = 30 m.
D. BC = 20 m.
Tại điểm O trong môi trường đẳng hướng không hấp thụ âm và phản xạ âm, phát ra âm với công suất không đổi. Trên tia Ox theo thứ tự có ba điểm A, B, C sao cho OC = 4OA. Biết mức cường độ âm tại B là 2 B, tổng mức cường độ âm tại A và C là 4 B. Nếu AB = 20 m thì
A. BC = 40 m
B. BC = 80 m
C. BC = 30 m
D. BC = 20 m
Tại điểm O trong môi trường đẳng hướng không hấp thụ âm và phản xạ âm, phát ra âm với công suất không đổi. Trên tia Ox theo thứ tự có ba điểm A, B, C sao cho OC = 4OA. Biết mức cường độ âm tại B là 2 B, tổng mức cường độ âm tại A và C là 4 B. Nếu AB = 20 m thì
A. BC = 40 m
B. BC = 80 m
C. 30 m
D. 20 m
Đặt mức cường độ âm ở A là x (B) thì mức cường độ âm ở C là 4 –x (B).
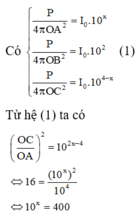

Cho các số thực không âm a, b, c thay đổi thỏa mãn \(a^2+b^2+c^2=1\). Tìm GTLN và GTNN của biểu thức \(Q=\sqrt{a+b}+\sqrt{b+c}+\sqrt{c+a}\)
Tham khảo:
Với các số thực không âm a,b,c thỏa mãn \(a^2+b^2+c^2=1\), tìm giá trị lớn nhất, giá trị nhỏ nhất của biểu thức: \(Q=\s... - Hoc24