Cho hình vẽ:
CM: a) \(\widehat{B}=\widehat{B}\) ; b) \(\Delta ABC=\Delta A'B'C'\)
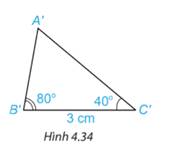
Vẽ thêm tam giác \({A^\prime }{B^\prime }{C^\prime }\) sao cho \({B^\prime }{C^\prime } = 3\;{\rm{cm}}\), \(\widehat {{A^\prime }{B^\prime }{C^\prime }} = {80^\circ },\widehat {{A^\prime }{C^\prime }{B^\prime }} = {40^\circ }.({\rm{H}}.4.34)\).
Dùng thước thẳng có vạch chia hoặc compa so sánh độ dài các cạnh của hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\).
Hai tam giác A B C và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau không?
A’B’=2,2 cm
A’C’=3,4 cm
Hai tam giác \(ABC\) và \({A^\prime }{B^\prime }{C^\prime }\) có bằng nhau.
1.Cho hình 16:
a) Cho biết \(Ax//Cy.So\) \(sánh \)\(\widehat{ABC}\) với \(\widehat{A}\) và \(\widehat{C}\)
b) Cho biết \(\widehat{ABC}\)=\(\widehat{A}\) và\(\widehat{C}\) . Chứng tỏ rằng \(Ax//\) Cy
1. Cho hình vẽ , biết
a // b ; c ⊥ a và \(\widehat{DCB}\) = 30'( độ ) . Tính \(\widehat{D_1}\) và \(\widehat{B_2}\)
Cho tam giác ABC có \(\widehat{A}\) = 120°, b = 8 cm, c = 5 cm. Tính a, \(\widehat{B}\), \(\widehat{C}\), ha, mc, S, R, r
1. Cho hình vẽ . Biết \(\widehat{A}\) = 135'( độ ) , \(\widehat{B}\) = 45'( độ ) , \(\widehat{D}\) = 55'( độ )
a) Đường thẳng a có song song với đường b không ? Vì sao ?
b) Tính số đo góc C\(_1\)
a) A + B = 180 độ
Mà A và B là cặp góc trong cùng phía
=> a//b
b) a//b
=> D = C (so le trong)
=> C = 55 độ
Cho hình vẽ . Biết \(\widehat{A}\) = 147'( độ ) , \(\widehat{B}\) = 33'( độ ) , \(\widehat{D}\) = 59'( độ )
a) Đường thẳng a có song song vưới đường thẳng b không ? Vì sao ?
b) Tính số đo góc C \(_1\) ?
\(\widehat{D1}=\widehat{C1}\left(soletrong\right)\)
\(\widehat{A1}+\widehat{B1}=180^o\left(bùnhau\right)\)
\(\Rightarrow\)a//b
\(\widehat{D1}=\widehat{C1}\left(soletrong\right)=59^o\)
Cho tam giác ABC có các cạnh a=BC; b=AC; c=AB. CMR:
a) \(a\widehat{A}+b\widehat{B}\ge a\widehat{B}+b\widehat{A}\)
b) \(a\widehat{A}+b\widehat{B}+c\widehat{C}\ge60^0\left(a+b+c\right)\)
c) \(a\left(\widehat{A}-60^0\right)+b\left(\widehat{B}-60^0\right)+c\left(\widehat{C}-60^0\right)\ge0\)
d) \(\frac{a\widehat{A}+b\widehat{B}}{\widehat{A}+\widehat{B}}+\frac{b\widehat{B}+c\widehat{C}}{\widehat{B}+\widehat{C}}+\frac{c\widehat{C}+a\widehat{A}}{\widehat{C}+\widehat{A}}\ge a+b+c\)
e) \(\frac{\left(a-b\right)\widehat{B}}{\widehat{A}+\widehat{B}}+\frac{\left(b-c\right)\widehat{C}}{\widehat{B}+\widehat{C}}+\frac{\left(c-a\right)\widehat{A}}{\widehat{C}+\widehat{A}}\le0\)
f) \(\frac{a\widehat{A}+b\widehat{B}+c\widehat{C}}{a+b+c}< 90^0\)
Cho hình vẽ : Biết a// BC và b// AC ,\(\widehat{AMB}\)=43 độ.
a)Tính\(\widehat{ACB}\)
b)C/m Rằng : \(\widehat{MBC}=\widehat{MAC}\)
Hình Vẽ : file:///D:/My%20Documents/Downloads/New%20Bitmap%20Image.bmp
Cho tam giác ABC có \(\widehat{A}>\widehat{B}>\widehat{C}\). Vẽ đường cao AH, lấy điểm O nằm giữa A và H. Tia CO cắt AB tại D.
a, CM: \(\widehat{B}\) và \(\widehat{C}\) nhọn.
b, So sánh: OB và OC.
c, So sánh OD và HD.
Help me!!! MK cần gấp lắm!!!
a) vì góc A lớn nhất nên góc A có thể là góc vuông, góc tù hoặc góc nhọn.
+trường hợp A là góc vuông và góc tù thì góc B và C ko thể lớn hơn hoặc bằng 90 độ. do đó góc B và C là góc nhọn
+ trường hợp góc A là góc nhọn thì góc B và góc C cx bé hơn 90 độ vì góc A>góc B> góc C.
a) Ta có: góc A> góc B> góc C
\(\Rightarrow\) góc B và góc C là góc nhọn
Tức quá , lag chết đi đc
b) Xét tam giác ABC có góc B > góc C
=> AC>AB (...........)
=> HC>HB ( quan hệ đường xiên hình chiếu )
=> OC>OB ( quan hệ đường xiên hình chiếu )
c) Xét tam giác OHC vuông tại H có :
góc HOC + góc HCO = 90 độ
=> góc HOC là góc nhọn
Ta có : góc HOC + góc HOD = 180 độ ( kề bù )
mà góc HOC là góc nhọn
=> góc HOD là góc tù
Xét tam giác OHD có góc HOD là góc tù
=> HD>OD ( quan hệ giữa góc và cạnh trong một tam giác)
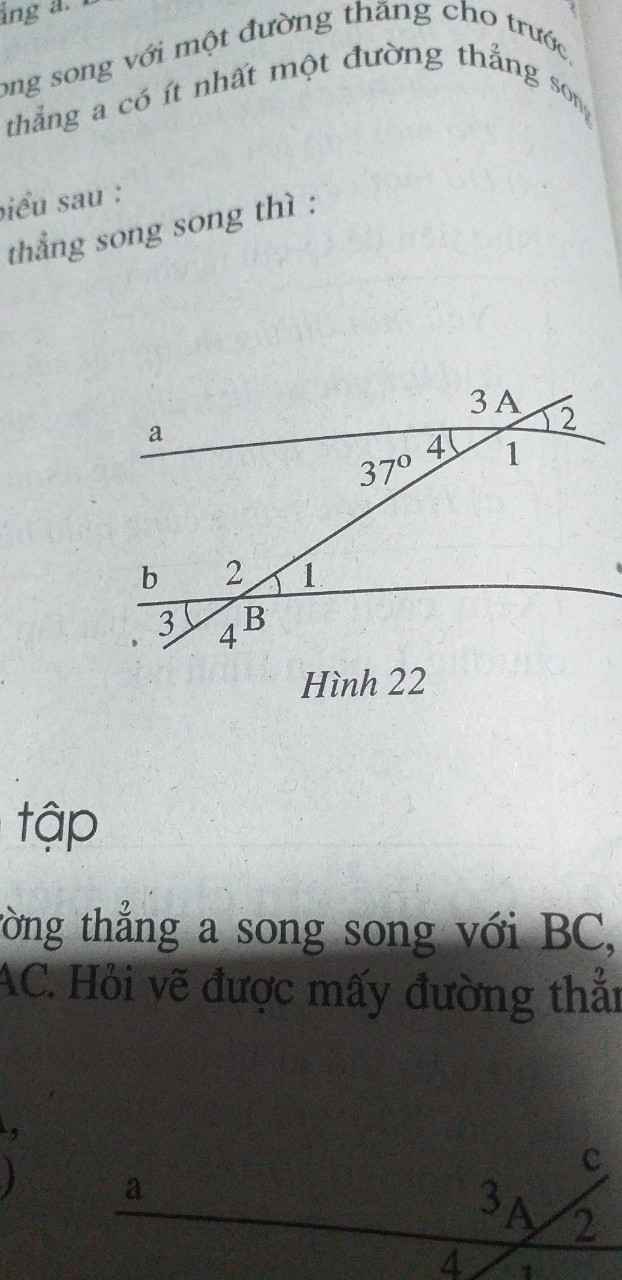
Hình 22 cho biết a // b và \(\widehat{A}_4\) = \(37^o\) .
a) Tính \(\widehat{B_1}\) .
b) So sánh \(\widehat{A_1}\) và \(\widehat{B_4}\) .
c) Tính \(\widehat{B_2}\)