Cho vectơ b → ≠ 0 ; a → = - 2 b → ; c → = a → + b → Khẳng định nào sau đây sai?
A. Hai vectơ ![]() bằng nhau.
bằng nhau.
B. Hai vectơ ![]() ngược hướng.
ngược hướng.
C. Hai vectơ ![]() cùng phương.
cùng phương.
D. Hai vectơ ![]() đối nhau.
đối nhau.
Cho đoạn thẳng AB có trung điểm I . Gọi M là trung điểm đoạn IB. Khẳng định nào sau đây đúng? A. Vectơ AM - 3 vectơ BM = vectơ 0 B. Vectơ AM + 3 vectơ MB = vectơ 0 C. Vectơ MA +3 vectơ BM = vectơ 0 D. Vectơ AM + 3 vectơ BM = vectơ 0 ( Giải chi tiết giúp mình ạ )
ta có: I là trung điểm của AB
=>\(IA=IB=\dfrac{AB}{2}\)
M là trung điểm của IB
=>\(MI=MB=\dfrac{IB}{2}=\dfrac{AB}{4}\)
AM=AI+IM=1/2AB+1/4AB=3/4AB
=>AM=MB
=>\(\overrightarrow{AM}=3\overrightarrow{MB}\)
=>\(\overrightarrow{AM}-3\overrightarrow{MB}=\overrightarrow{0}\)
=>\(\overrightarrow{AM}+3\overrightarrow{BM}=\overrightarrow{0}\)
=>Chọn C
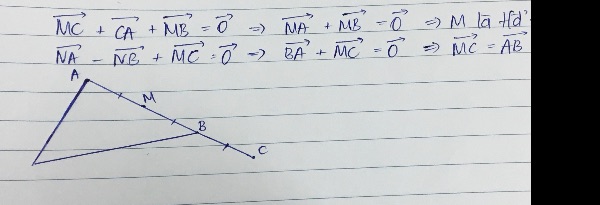
Cho vectơ a = (2; -2), vectơ b = (1; 4). Hãy phân tích vectơ c (5; 0) theo hai vectơ a và b.
Cho tam giác ABC lấy M, N ,P sao cho vectơ MB = 3 vectơ MC ; vectơ Na + 3 vectơ NC = vectơ 0 và vectơ P A + vectơ PB = vectơ 0
a) tính vectơ PM và vectơ PN theo vectơ AB ; vectơ AC
b) Chứng minh rằng M, N,P thẳng hàng
Cho vectơ a, b là hai vectơ khác vectơ 0. Khi nào có đẳng thức
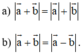
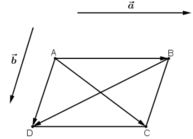
Có hai vec tơ a→, b→ bất kì như hình vẽ.
Vẽ hình bình hành ABCD sao cho 
Ta có:
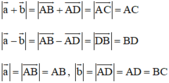
Do đó
a) 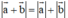 ⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ AC = AB + BC ⇔ B nằm giữa A và C
⇔ 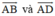 cùng hướng hay a→ và b→ cùng hướng.
cùng hướng hay a→ và b→ cùng hướng.
b) 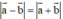 ⇔ AC = BD
⇔ AC = BD
⇔ ABCD là hình chữ nhật
⇔ AB ⊥ CD hay 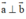
Cho tam giác ABC có D, E, F là trung điểm của BC CA AB chứng minh rằng
a, vectơ AD + vectơ BE + vectơ CF = vectơ 0
b với mọi m vectơ MA+ vectơ MB + vectơ MC = vectơ MD + vectơ ME + vectơ MF
Lời giải:
a)
$2\overrightarrow{AD}=\overrightarrow{AD}+\overrightarrow{AD}$
$=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{AC}+\overrightarrow{CD}$
$=\overrightarrow{AB}+\overrightarrow{AC}+(\overrightarrow{BD}+\overrightarrow{CD})$
$=\overrightarrow{AB}+\overrightarrow{AC}$
$\Rightarrow \overrightarrow{AD}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}$
Tương tự:
$\overrightarrow{BE}=\frac{\overrightarrow{BC}+\overrightarrow{BA}}{2}$
$\overrightarrow{CF}=\frac{\overrightarrow{CA}+\overrightarrow{CB}}{2}$
Cộng lại:
$\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF}=\frac{\overrightarrow{AB}+\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\frac{\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}}{2}=\overrightarrow{0$}$
Ta có đpcm.
b)
$\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{MD}+\overrightarrow{DA}+\overrightarrow{ME}+\overrightarrow{EB}+\overrightarrow{MF}+\overrightarrow{FC}$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})+(\overrightarrow{DA}+\overrightarrow{EB}+\overrightarrow{FC})$
$=(\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF})-(\overrightarrow{AD}+\overrightarrow{BE}+\overrightarrow{CF})$
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}-\overrightarrow{0}$ (theo phần a)
$=\overrightarrow{MD}+\overrightarrow{ME}+\overrightarrow{MF}$
Ta có đpcm.
Cho tam giác DEF. Gọi M,N,P lần lượt là trung điểm DE,EF, FD a/ chứng minh các vectơ EP=EM+EN b/ vectơ ME+NF+PD=0 c/ vectơ DN+EP+FM=0
Cho hai vectơ a → và b → khác 0 → . Xác định góc α giữa hai vectơ a → và b → khi a → . b → = − a → . b → .
A. α = 180 0 .
B. α = 0 0 .
C. α = 90 0 .
D. α = 45 0 .
Ta có a → . b → = a → . b → . c o s a → , b → .
Mà theo giả thiết a → . b → = − a → . b →
Suy ra cos a → , b → = − 1 ⇒ a → , b → = 180 0 .
Chọn A.
Cho △ABC. Gọi M,N,P lần lượt là trung điểm BC,CA,AB. a) vectơBM + vectơCN + vectơAP = vectơ 0. b)vectơAP + vectơAN - vectơAC + vectơ BM = vectơ 0. c)vectơOA + vectơOB + vectơOC = vectơOM + vectơON + vectơOP
a) Ta có: \(\overrightarrow{BM}+\overrightarrow{CN}+\overrightarrow{AP}=\frac{\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}}{2}=\frac{\overrightarrow{BB}}{2}=\overrightarrow{0}\)
b) Ta có: \(\overrightarrow{AP}+\overrightarrow{AN}-\overrightarrow{AC}+\overrightarrow{BM}=\overrightarrow{AP}+\overrightarrow{CN}+\overrightarrow{BM}=\overrightarrow{0}\)(theo câu a)
c) Ta có: \(\overrightarrow{OA}-\overrightarrow{OP}=\overrightarrow{PA}\); \(\overrightarrow{OB}-\overrightarrow{OM}=\overrightarrow{MB}\);\(\overrightarrow{OC}-\overrightarrow{ON}=\overrightarrow{NC}\)
Cộng vế theo vế ta được \(\left(\overrightarrow{OA}-\overrightarrow{OP}\right)+\left(\overrightarrow{OB}-\overrightarrow{OM}\right)+\left(\overrightarrow{OC}-\overrightarrow{ON}\right)=\overrightarrow{PA}+\overrightarrow{MB}+\overrightarrow{NC}=\frac{\overrightarrow{BA}+\overrightarrow{AC}+\overrightarrow{CB}}{2}=\frac{\overrightarrow{BB}}{2}=\overrightarrow{0}\)
Chuyển vế suy ra điều phải chứng minh
mấy bài trên rất cơ bản chỉ cần dùng quy tắc ba điểm và quy tắc hiệu là có thể giải một cách dễ dàng