Câu 4: Cho đường tròn (O; R). Từ điểm M ở ngoài đường tròn vẽ các tiếp tuyến MA, MB (với A, B là hai tiếp điểm) và kẻ đường kính AC của đường tròn.
a) Chứng minh rằng tứ giác MAOB nội tiếp.
b) Cho OM = 5 cm, tính độ dài đường tròn ngoại tiếp tứ giác MAOB (với ≈ 3,14).
c) Gọi D là giao điểm của tia CB và tia AM. Chứng minh rằng MBD = MDB.
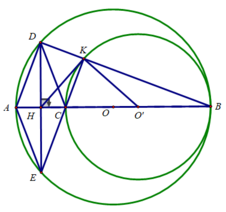
Câu 5: Cho ∆ABC có các góc A, B, C đều nhọn nội tiếp đường tròn (O). Gọi d là tiếp tuyến tại A của đường tròn (O). Các đường cao AI và BK của ∆ABC cắt nhau tại H. Đường thẳng BK kéo dài cắt đường tròn (O) tại D và cắt đường thẳng d tại E
a. Chứng minh ABIK, HKCI là các tứ giác nội tiếp.
b. Chứngminh: AE² = BE.DE Làm ơn giúp mik vs ạ . Mik đag cần gấp 😭