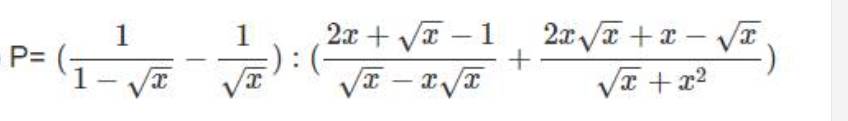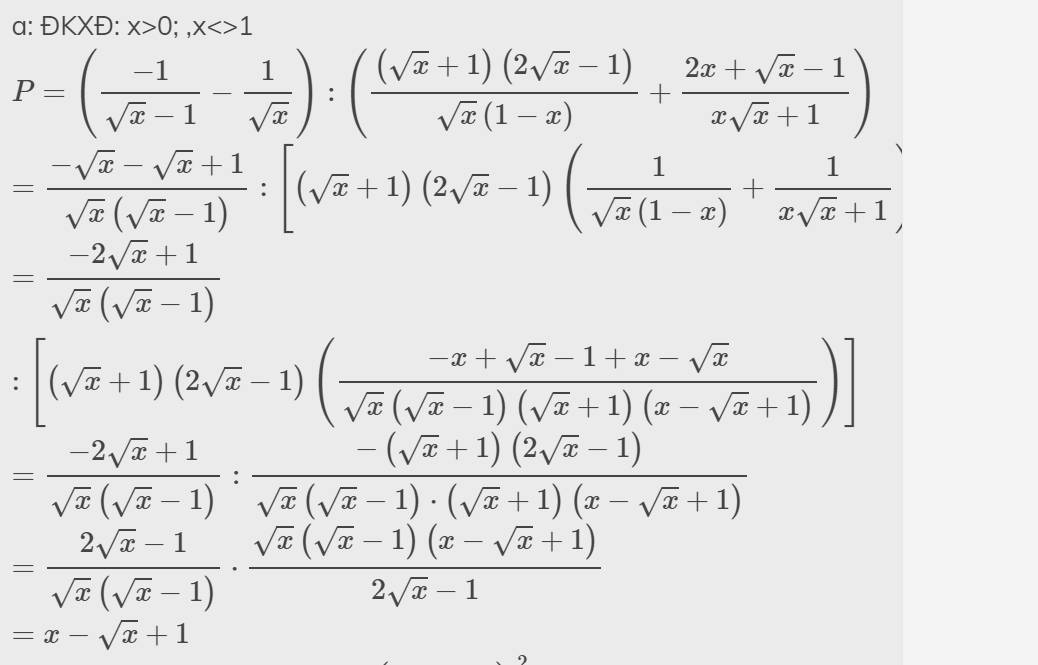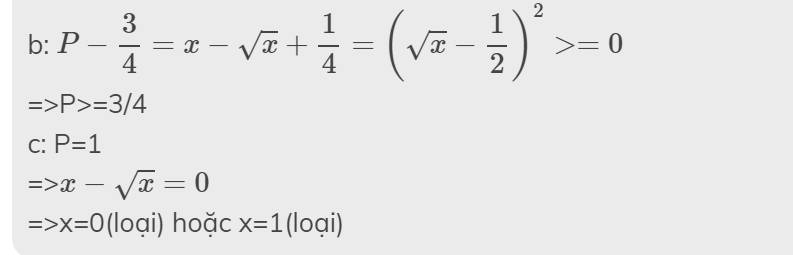Cho P = \(\dfrac{1}{\sqrt{x}-1}\); Q = \(\dfrac{1}{\sqrt{x}+1}\)(ĐKXĐ: x ≥ 0; x ≠ 1). Tìm x thỏa mãn: \(\dfrac{1}{Q}+P\le4\)
NN
Những câu hỏi liên quan
Cho P: \(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
CMR: P=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
\(P=\left(\dfrac{x-2+\sqrt{x}}{\left(\sqrt{x}+2\right)\left(\sqrt{x}\right)}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
Đúng 0
Bình luận (0)
Cho P = (\(\dfrac{1}{\sqrt{x}-1 }\) - \(\dfrac{1}{\sqrt{x}}\))(\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\) - \(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\))
a. Tìm đkxđ và rút gọn P
b. Tìm x để P = \(\dfrac{1}{4}\)
Điều kiện: x>2
P= \(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{2}+2}{\sqrt{x}-1}\right)\)
P= \(\left(\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{x-1-x+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\right)\)
P= \(\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{3}\)
P= \(\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
b) P= \(\dfrac{1}{4}\)
⇔\(\dfrac{\sqrt{x}-2}{3\sqrt{x}}\) =\(\dfrac{1}{4}\)
⇔\(4\sqrt{x}-8=3\sqrt{x}\)
⇔\(\sqrt{x}=8\)
⇔x=64 (TM)
Vậy X=64(TMĐK) thì P=\(\dfrac{1}{4}\)
Đúng 3
Bình luận (0)
Cho P= \((\dfrac{1}{1-\sqrt{2}}-\dfrac{1}{\sqrt{x}}):(\dfrac{2x+\sqrt{x}-1}{\sqrt{x}-x\sqrt{x}}+\dfrac{2x\sqrt{x}+x-\sqrt{x}}{\sqrt{x}+x^{2}})\)
a) Rút gọn P
b) so sánh P với \(\dfrac{3}{4}\).
c) tìm x để P=1
cho 2 biểu thức M =\(\dfrac{\sqrt{x}-1}{\sqrt{x}}\)
P=\(\dfrac{\sqrt{x}+6}{\sqrt{x}-1}\)+\(\dfrac{2-8\sqrt{x}}{x-1}\)-\(\dfrac{2}{1-\sqrt{x}}\)
cho bt
P=(\(\dfrac{1}{\sqrt{x}-1}\)-\(\dfrac{1}{\sqrt{x}}\)):(\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\)-\(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\))
a)Tìm đk của x để P xác định
b)Rút gọn P
c)Tìm xđể P=\(\dfrac{1}{4}\)
\(a,P\) xác định \(\Leftrightarrow\left[{}\begin{matrix}x>0\\x\ne1\\x\ne4\end{matrix}\right.\)
\(b,P=\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\\ =\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\\ =\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{x-1-x+4}\\ =\dfrac{1}{\sqrt{x}}.\dfrac{\sqrt{x}-2}{3}\\ =\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
\(c,P=\dfrac{1}{4}\Leftrightarrow\dfrac{\sqrt{x}-2}{3\sqrt{x}}=\dfrac{1}{4}\\ \Leftrightarrow\dfrac{4\left(\sqrt{x}-2\right)-3\sqrt{x}}{12\sqrt{x}}=0\\ \Leftrightarrow4\sqrt{x}-8-3\sqrt{x}=0\\ \Leftrightarrow\sqrt{x}=8\\ \Leftrightarrow x=64\left(tmdk\right)\)
Vậy \(x=64\) thì \(P=\dfrac{1}{4}\)
Đúng 2
Bình luận (0)
Cho P=\(\dfrac{2}{\left(x+1\right)\sqrt{x+1}+\left(x-1\right)\sqrt{x-1}}.\dfrac{\dfrac{2x}{\sqrt{x-1}}-\sqrt{x+1}}{\dfrac{1}{\sqrt{x-1}}-\dfrac{1}{\sqrt{x+1}}}\). với x>1
Tìm x để P=x-1
Cho pleft(dfrac{x-2}{x+2sqrt{x}}+dfrac{1}{sqrt{x}+2}right).dfrac{sqrt{x}+1}{sqrt{x}-1}với x0 và xne1
a) cm pdfrac{sqrt{x}+1}{sqrt{x}}
b) Tìm các giá trị của x để cho Adfrac{1}{1+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+dfrac{1}{sqrt{3}+sqrt{4}}+...+dfrac{1}{sqrt{120}+sqrt{121}}
B1+dfrac{1}{sqrt{2}}+...+dfrac{1}{sqrt{35}} Chứng minh rằng BA
Đọc tiếp
Cho p=\(\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)với x>0 và x\(\ne\)1
a) cm p=\(\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
b) Tìm các giá trị của x để cho A=\(\dfrac{1}{1+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{120}+\sqrt{121}}\)
B=\(1+\dfrac{1}{\sqrt{2}}+...+\dfrac{1}{\sqrt{35}}\) Chứng minh rằng B>A
mọi người ơi giải giúp mình một tí đang cần gấp
Đúng 0
Bình luận (0)
Cho hai biểu thức:
A = \(\dfrac{2x+3\sqrt{x}}{x\sqrt{x}+1}+\dfrac{1}{x-\sqrt{x}+1}-\dfrac{1}{\sqrt{x}+1}\) và B = \(\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\) với \(x\ge0;x\ne4;x\ne9\)
c) Biểu thức P = A.B sau khi thu gọn được P = \(\dfrac{\sqrt{x}+5}{\sqrt{x}+1}\). Tìm các số tự nhiên x để P nhận giá trị nguyên
c: P nguyên
=>căn x+1+4 chia hết cho căn x+1
=>căn x+1 thuộc {1;2;4}
=>x thuộc {1;9}
Đúng 1
Bình luận (0)
Cho 3 số dương x,y,z. CMR:\(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}+\dfrac{1}{\sqrt{z}}>=3\left(\dfrac{1}{\sqrt{x}+2\sqrt{y}}+\dfrac{1}{\sqrt{y}+2\sqrt{z}}+\dfrac{1}{\sqrt{z}+2\sqrt{x}}\right)\)
Áp dụng BĐT Cauchy-Schwarz ta có:
\(\dfrac{1}{\sqrt{x}+2\sqrt{y}}\le\dfrac{1}{9}\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}+\dfrac{1}{\sqrt{y}}\right)\)
Tương tự cho 2 BĐT trên ta có:
\(\dfrac{1}{3}VP\le\dfrac{1}{9}\cdot3\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}+\dfrac{1}{\sqrt{z}}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{\sqrt{x}}+\dfrac{1}{\sqrt{y}}+\dfrac{1}{\sqrt{z}}\right)=\dfrac{1}{3}VT\)
Xảy ra khi \(x=y=z\)
Đúng 0
Bình luận (0)
Cho biểu thức A=\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
a) Tìm điều kiện xác định
b) Rút gọn biểu thức
c) CMR: A>0 với mọi x \(\ne\)1
d) Tìm x để A đạt GTLN,tìm x để A đạt GTLN đó
Đúng 0
Bình luận (0)