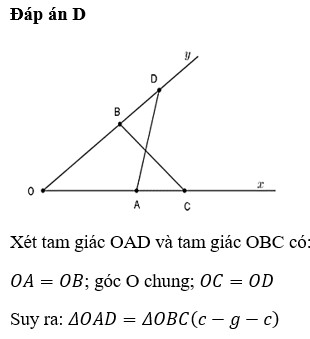
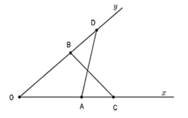
Cho góc nhọn x0y. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC; OB = OD. Gọi I là giao điểm c ủa AD và BC.Chứng minh:
a) OI là tia phân giác của góc xOy.
b) Gọi M, N lần lượt là trung điểm của AC và BD. Chứng minh M, I, N thẳng hàng.