Cho hình vuông ABCD. Gọi các điểm E và F lần lượt là trung điểm của cạnh AB và BC; M là giao điểm của CE và DF.
a) Chứng minh CE ⊥ DF.
b) Chứng minh AM = CD.
c) Gọi P là trung điểm của cạnh CD. Chứng minh ∆AMP vuông.
Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF. Tính diện tích tam giác MDC theo a
Xét tam giác vuông là tam giác BEC và tam giác DCF có CD = BC , BE = CF = 1/2a
=> Tam giác BEC = tam giác DCF (hai cạnh góc vuông)
=> góc CDF = góc BCE mà góc CDF + góc DFC = 90 độ
=> góc ECF + góc DFC = 90 độ hay góc DMC = 90 độ => CE vuông góc DF
Ta chứng minh được tam giác MDC đồng dạng tam giác CDF (g.g)
Áp dụng định lí Pytago có \(DF=\sqrt{CD^2+FC^2}=\sqrt{a^2+\frac{a^2}{4}}=\frac{a\sqrt{5}}{2}\)
\(S_{CDF}=\frac{1}{2}CD.CF=\frac{1}{2}a.\left(\frac{a}{2}\right)=\frac{a^2}{4}\)
Suy ra \(\frac{S_{MDC}}{S_{CDF}}=\left(\frac{CD}{DF}\right)^2=\left(\frac{a}{\frac{a\sqrt{5}}{2}}\right)^2=\left(\frac{2}{\sqrt{5}}\right)^2=\frac{4}{5}\)
\(\Rightarrow S_{MDC}=\frac{4}{5}S_{CDF}=\frac{4}{5}.\frac{a^2}{4}=\frac{a^2}{5}\)
cho hình vuông ABCD gọi M,N,P,Q lần lượt là trung điểm của các cạnh AB,BC,CD,DA.gọi E,H lần lượt là giao điểm của AP với BQ và DN; F,G lần lượt là giao điểm của CM với BQ và DN. CMinh AP//CM và góc DAP =góc CDN
Cho hình vuông ABCD có cạnh bằng a. Gọi E, F lần lượt là trung điểm các cạnh AB,BC . Gọi M là giao điểm của CE và DF .A. c/m góc ECB = góc CDF và CE vuông góc DF B.c/m CM.CECF =a C. Gọi K là giao điểm của CM và DA . C/m tam giác MAD cân

a: Xét tứ giác BECF có
D là trung điểm chung của BC và EF
BE=EC
Do đó: BECF là hình thoi
b: Sửa đề: Tính diện tích BECF
\(BC=\sqrt{10^2-8^2}=6\left(cm\right)\)
DE=AB/2=4cm
=>EF=8cm
\(S_{BECF}=\dfrac{1}{2}\cdot6\cdot8=3\cdot8=24\left(cm^2\right)\)
Cho hình vuông ABCD có cạnh bằng a. Gọi E;F;G;H lần lượt là trung điểm của các cạnh AB;BC;CD;DA. Gọi M là giao điểm của CE và DF.
a) Chứng minh: EFGH là hình vuông.
b) Chứng minh: DF vuông góc CE và tam giác MAD cân
c) Tính diện tích tam giác MDC theo a
Cho hình vuông ABCD tâm I. gọi E, F, G, H lần lượt là trung điểm của các cạnh DA, AB, BC, CD. Phép đối xứng trục AC biến:
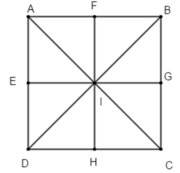
A. ∆IED thành ∆IGC
B. ∆IFB thành ∆IGB
C. ∆IBG thành ∆IDH
D. ∆IGC thành ∆IFA
Tìm ảnh của từng điểm qua phép đối xứng trục AC: điểm I biến thành I; B thành D; G thành H.
Chọn đáp án C
Cho tam giác ABC. Trên hai cạnh AB, AC lấy hai điểm E, F sao cho EF ∥ BC. Gọi H, G lần lượt là hình chiếu vuông góc của E, F lên BC. Gọi M, N lần lượt là trung điểm của BC và đường cao AI. Chứng minh rằng BN đi qua trung điểm của EH và MN đi qua trung điểm của HF.
Gọi P là giao của BN với EH; Q là giao của MN với HF; K là giao của MN với EF
Ta có
\(EH\perp BC;AI\perp BC\)=> EH//AI \(\Rightarrow\frac{PE}{NA}=\frac{PH}{NI}\) (Talet) \(\Rightarrow\frac{PE}{PH}=\frac{NA}{NI}=1\Rightarrow PE=PH\)
=> BN đi qua trung điểm P của EH
Ta có
EF//BC (gt) => KF//HM \(\Rightarrow\frac{QK}{QM}=\frac{QF}{QH}=\frac{KF}{HM}\) (Talet) => KH//FM
Xét tứ giác KFMH có
KF//HM; KH//FM => KFMH là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)
=> KF=HM (Trong hình bình hành các cạnh đối bằng nhau)
\(\Rightarrow\frac{QF}{QH}=\frac{KF}{HM}=1\Rightarrow QF=QH\)
=> MN đi qua trung điểm Q của HF
Cho hình chữ nhật ABCD, các điểm M, N, P, Q lần lượt là trung điểm của cạnh AB, BC, CD, DA. Các điểm E, F, G, H lần lượt là trung điểm các cạnh MN, NP, PQ và QM. Tính tỉ số diện tích của hình chữ nhật EFGH và hình chữ nhật ABCD.
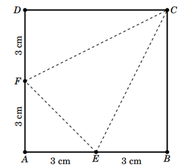
Cho hình vuông ABCD có cạnh bằng 6 cm. Gọi E, F lần lượt là trung điểm của các cạnh AB và AD. Gấp hình vuông trên để được tứ diện ACEF. Thể tích khối tứ diện ACEF là
A. 18 cm 3 .
B. 3 cm 3 .
C. 27 cm 3 .
D. 9 cm 3 .
Cho hình vuông ABCD có các cạn bằng a . Các điểm E <, F lần lượt là trung điểm của AB, BC . Gọi O là giao điểm của CE và DF . Chứng minh rằng CE.CM / CF =a