Cho ΔABC = ΔDEG. Biết DE = 15cm; Ê = \(70^o\) và Â − Ĉ = \(40^o\) .
a) Tính số đo các góc của hai tam giác.
b) Tính AB.
Cho ΔABC = ΔDEG. Biết DE = 15cm; E = \(70^o\) và A - C = \(40^o\)
a) Tính số đo các góc của hai tam giác.
b) Tính AB.
cho ΔDEF∼ΔABC. Biết AB=12cm, BC=15cm và DE=4cm. độ dài đoạn thẳng EF là
Ta có tỉ số : \(\dfrac{DE}{AB}=\dfrac{EF}{BC}\Rightarrow\dfrac{4}{12}=\dfrac{EF}{15}\Rightarrow EF=\dfrac{15\times4}{12}=5\)
Vậy \(EF=5cm\)
Cho tam giác ABC AB =9cm, AC = 12 cmvà BC = 15cm. Tia phân giác góc C cắt AB tại D. Kẻ DE ![]() BC (E
BC (E![]() BC).
BC).
a) ΔABC là tam giác gi? Vì sao b) Chứng minh AC = CE c)Trên tia AB lấy điểm F sao cho AF = AC. Kẻ tia Fx ![]() FA cắt tia DE tại M. Tính
FA cắt tia DE tại M. Tính
Cho ΔABC, đường phân giác góc B cắt AC tại D và cho biết AB = 10cm, BC = 15cm, AD = 6cm. Tính AC = ?
A. 6cm
B. 9cm
C. 12cm
D. 15cm
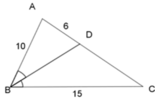
Áp dụng tính chất đường phân giác trong tam giác ABC, ta có: B A A D = B C C D
⇒ 10 6 = 15 C D ⇔ C D = 6.15 10 = 9 c m
=> AC = AD + DC = 6 + 9 = 15cm
Đáp án: D
Cho ΔABC vuông tại A có đường cao AH, biết AB = 15cm , AC = 20cm.
a) Chứng minh: ΔHBA và ΔABC đồng dạng.
b) Tính độ dài BC và AH.
c) Chứng minh: AH^2 = HB.HC
Ai biết thì giúp mình với ạ. Xin cảm ơn ạ
a) Xét ΔHBA và ΔABC có:
^A=^H=90o
^HAB=^ACB(cùng phụ với ^ABC)
→ ΔHBA∼ΔABC(g.g)
b) Áp dụng định lí Pytago vào tam giác vuông ABC, ta có:
\(BC=\sqrt{20^2+15^2}=25cm\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}AB.AC\)
\(\rightarrow AH.BC=AB.AC\)
\(\rightarrow AH=\dfrac{AB.AC}{BC}=12cm\)
c) Xét ΔAHB và ΔCHA có:
^AHB=^CHA=90o
^HCA=^HAB(cùng phụ với ^ABC)
→ ΔAHB∼ΔCHA(g.g)
\(\rightarrow\dfrac{AH}{HB}=\dfrac{HC}{AH}\left(tươngứng\right)\)
\(\rightarrow AH^2=HB.HC\)
ΔABC vuông ở A , đường cao AH
a) C/m ΔABC ∼ ΔHBA
b) Biết AB =8cm , AC=15cm . Tính BC
c) Tính HB , HC
a.Xét tam giác ABC và tam giác HBA có:
^B chung
^BAC = ^BHA = 90
=> tam giác ABC ~ tam giác HBA (g.g)
b. Áp dụng đl Pytago cho tam giác ABC vuông tại A:
BC2=AB2+AC2=82+152=289
=>BC=17cm
c.tam giác ABC ~ tam giác HBA
=> AB/HB=BC/BA
=>HB=AB2/BC=82/17=64/17 cm
=>HC=BC-HB=225/17
Bài 1: Cho 2 tam giác vuông, ΔABC vuông tại A, MNP vuông tại M. Biết ΔABC = ΔMNP, AB= 20cm, AC= 15cm. Tính các cạnh của ΔMNP
Bài 2: Cho ΔABC có AB=AC. Gọi H là trung điểm của cạnh BC a) Chứng minh ΔABH = ΔACH b) Chứng minh AH vuông ∠ BC c) Trên tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Chứng minh ΔHAD = ΔHAE d) Gọi K là trung điểm của DE. Chứng minh 3 điểm A, H, K thẳng hàng
ANH CHỊ GIÚP EM VỚI CHIỀU EM NỘP RỒI
Cho ΔDEF ∼ ΔABC biết DE = 5cm, AB = 6cm, AC = 12cm. Độ dài DF là:
A. 8cm
B. 9cm
C. 10cm
D. 15cm
Cho ΔABC nhọn (AC<AB). Vẽ AM vuông góc (M ϵ BC)biết AC=15 cm, AM= 12cm, MB=9cm. Tính chu vi △ABC.
Áp dụng định lý pitago vào tam giác vuông AMB,có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AB=\sqrt{12^2+9^2}=\sqrt{225}=15cm\)
Áp dụng định lý pitago vào tam giác vuông AMC, có:
\(AC^2=AM^2+CM^2\)
\(\Rightarrow CM=\sqrt{AC^2-AM^2}=\sqrt{15^2-12^2}=\sqrt{81}=9cm\)
\(C_{ABC}=AB+AC+BC=15+15+\left(9+9\right)=48cm\)
Áp dụng định lí Pytago ta có
\(AB^2=AM^2+MB^2\\ =\sqrt{12^2+9^2}=15\)
Chu vi tam giác ABC là
\(15+15+9+9=48\left(cm\right)\)