Cho tứ diện ABCD có A B = a ; D A B ^ = C B D ^ ; A C = a 5 ; A B C ^ = 135 o . Biết góc giữa hai mặt phẳng (ABD), (BCD) bằng 30o. Thể tích của tứ diện ABCD là
A. a 3 2 3
B. a 3 2
C. a 3 3 2
D. a 3 6
Cho tứ diện ABCD có A B , A C , A D đôi một vuông góc với nhau, A B = a , A C = b , A D = c . Tính thể tích V của khối tứ diện ABCD theo a, b, c
A. V = a b c 2
B. V = a b c 6
C. V = a b c 3
D. V = a b c
Đáp án B
V A . B C D = 1 3 A D . S A B C = 1 6 A B . A C . A D = a b c 6
Cho tứ diện ABCD có AB,AC,AD đôi một vuông góc với nhau, AB=a, AC=b, AD=c Tính thể tích V của khối tứ diện ABCD theo a, b, c
![]()
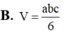
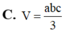
![]()
Cho tứ diện ABCD có AD = a, AB=b, AC=c. Thể tich của tứ diện theo a, b, c la?
Trong không gian tọa độ Oxyz, cho tứ diện ABCD có A(1;0;0), B(0;1;0), C(0;0;1), D(-2;1;-1). Thể tích của tứ diện ABCD bằng
A. 1
B. 2
C. 1 2
D. 1 3
Chọn đáp án C.
Ta có
![]()
![]()
Áp dụng công thức ta có:
V A B C D = 1 6 A B ⇀ . A C ⇀ . A D ⇀ = 1 2
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
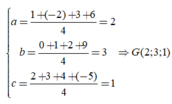
Trong không gian Oxyz, cho tứ diện ABCD có A ( 1 ; 0 ; 2 ) , B ( - 2 ; 1 ; 3 ) , C ( 3 ; 2 ; 4 ) , D ( 6 ; 9 ; - 5 ) . Tìm tọa độ trọng tâm G của tứ diện ABCD
A. G - 9 ; 18 4 ; - 30
B. G(8;12;4)
C. G 3 ; 3 ; 14 4
D. G(2;3;1)
Chọn D.
Gọi G(a,b,c) là trọng tâm của tứ diện, ta có:
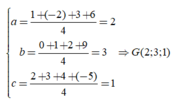
Cho tứ diện ABCD có A B = a 2 , A C = A D = a , B C = B D = a , C D = a . Tính thể tích V của khối tứ diện ABCD.
A. V = a 3 2 12
B. V = a 3 6 8
C. V = a 3 6 24
D. V = a 3 2 4
Chọn A
Gọi H là hình chiếu vuông góc của A trên (BCD). Khi đó CD vuông góc với mp(ABH).
Thể tích tứ diện ABCD gấp đôi thể tích của tứ diện ABCE, với E là trung điểm CD.
Cách khác: Gọi I là trung điểm AB.
Dễ thấy IACD và IBCD là các tứ diện vuông tại I, có các cạnh góc vuông là a 2
Cho tứ diện ABCD có A B = a 2 , AC=AD=a, BC=BD=a, CD=a. Tính thể tích V của khối tứ diện ABCD.
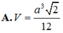
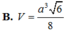
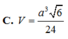
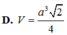
Cho tứ diện ABCD có AB=AC=AD=2a. Biết tam giác BCD có BC=2a, BD=a, C B D ^ = 120 ° . Tính thể tích tứ diện ABCD theo a
![]()
![]()
![]()
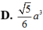
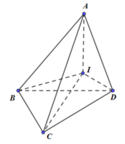
Cho tứ diện ABCD có AB = AC = AD = 2a. Biết tam giác BCD có BC = 2a, BD = a, C B D ^ = 120 0 . Tính thể tích tứ diện ABCD theo a.
A. 5 3 a 3
B. 5 2 a 3
C. 5 a 3
D. 5 6 a 3
Phương pháp:
Sử dụng các công thức diện tích tam giác ![]() và công thức Cosin
và công thức Cosin ![]()
Cách giải:
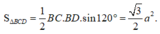
![]()
![]()
Ta có: ![]()
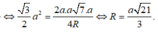
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD ![]()
![]()
Thể tích tứ diện ABCD là 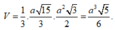
Chọn D.