Cho tam giác ABC. Vẽ ba đường phân giác AD; BE; CF cắt nhau tại O. Kẻ OG vuông góc BC tại G. Chứng minh rằng góc BOG = góc COD.
Mình được gợi ý là dùng góc ngoài. Mình cần cách giải gấp trong một tuần. Giúp mình nhé
TT
Những câu hỏi liên quan
Cho tam giác ABC. Từ C kẻ đường thẳng song song với đường phân giác AD của tam giác ABC, đường thẳng này cắt đường thẳng BA tại E
*Vẽ hình hộ mình đc rồi.Cảm ơn
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung trực của tam giác ABC.
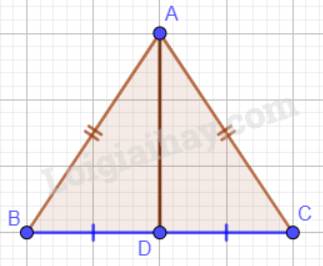
AD là phân giác của góc A nên \(\widehat {BAD} = \widehat {CAD}\).
Xét tam giác ABD và tam giác ACD có:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\);
AD chung
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c) nên \(BD = CD\) (2 cạnh tương ứng)
\(\Rightarrow\) D là trung điểm của cạnh BC.
Vì \(\Delta ABD = \Delta ACD\) nên \(\widehat {ADB} = \widehat {ADC}\) ( 2 góc tương ứng).
Mà \(\widehat {ADB} + \widehat {ADC}=180^0\) (2 góc kề bù) nên \(\widehat {ADB} = \widehat {ADC} = 90^\circ \Rightarrow AD \bot BC\).
Vậy AD là đường trung trực của tam giác ABC.
Đúng 0
Bình luận (0)
Cho tam giác ABC ( AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M.
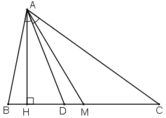
- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:
Đúng 0
Bình luận (0)
Cho tam giác ABC ; đường cao AH , vẽ AD, CK lần lượt là các đường phân giác của tam giác ABH; ABC; AD cắt CK tại E . a) chứng minh rằng tam giác ACD
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Chứng minh AD cũng là đường trung tuyến của tam giác đó.
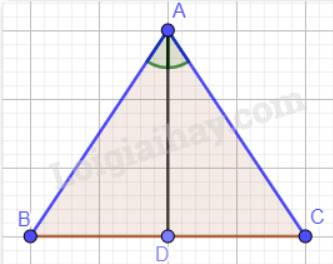
Xét hai tam giác ABD và ACD:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung.
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c).
Suy ra: BD = CD ( 2 cạnh tương ứng) hay D là trung điểm của cạnh BC. Vậy AD là đường trung tuyến của tam giác ABC.
Đúng 0
Bình luận (0)
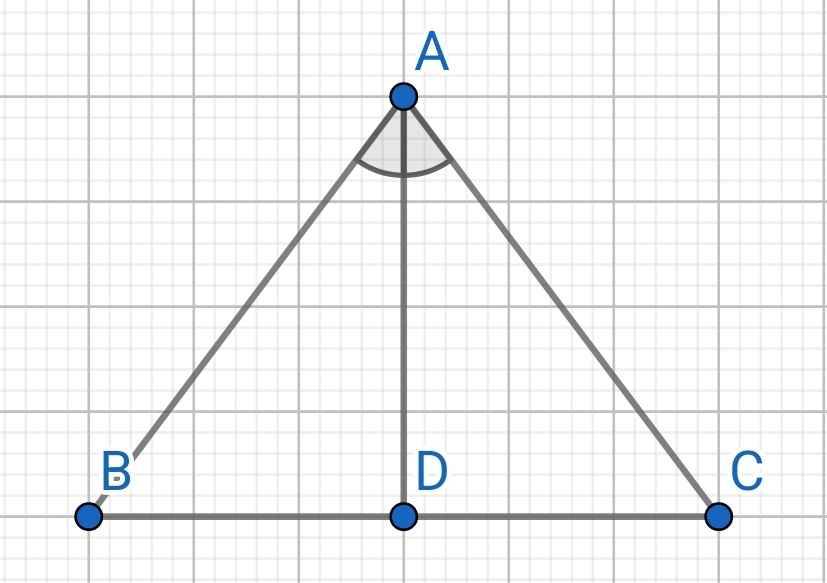Do ∆ABC cân tại A
⇒ AB = AC và ∠ABC = ∠ACB
⇒ ∠ABD = ∠ACD
Do AD là đường phân giác của ∠BAC
⇒ ∠BAD = ∠CAD
Xét ∆ABD và ∆ACD có:
∠BAD = ∠CAD (cmt)
AB = AC (cmt)
∠ABD = ∠ACD (cmt)
⇒ ∆ABD = ∆ACD (g-c-g)
⇒ BD = CD (hai cạnh tương ứng)
⇒ D là trung điểm của BC
Vậy AD là đường trung tuyến của ∆ABC
Đúng 0
Bình luận (0)
HH
29 tháng 3 2023 lúc 21:10
Cho tam giác ABC vuông tại A đường cao AH. Vẽ đường phân giác AD của tam giác CHA , đường phân giác BK của tam giác ABC. Gọi giao của BK và AH, AD lần lượt là E và F. a) chứng minh tam giác AHB đồng dạng với tam giác CHA b) chứng minh tam giác AEF đồng dạng với tam giác BEH c) chứng minh KD //AH d) eh/ad = ed/dc
a: Xét ΔAHB vuông tại H và ΔCHA vuông tạiH có
góc HAB=góc HCA
=>ΔAHB đồng dạng với ΔCHA
c: BK là phân giác
=>AK/CK=BA/BC
ΔAHC có AD là phân giác
nên DH/CD=AH/AC=BA/BC
=>DH/CD=AK/CK
=>KD//AH
Đúng 1
Bình luận (0)
Cho tam giác ABC . Từ C kẻ đường thẳng song song đường phân giác AD của ΔABC, đường thẳng này cắt đường thẳng BA tại E
Vẽ hình giùm mik
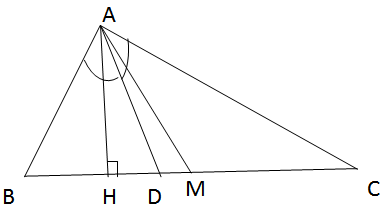
Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M ?
- Nhận xét: D luôn nằm giữa H và M.
- Chứng minh:
Đúng 0
Bình luận (0)
Δ AMB và Δ AMC có: AM chung MB =MC và AC > AB
=> AMC^ > AMB^ => M thuộc CH.(M ở giữa C và H)
AB<AC => B^ > C^ => BAH^ < CAH^ => D thuộc CH.(1)
theo tính chất phân giác:
BD/AB = CD/AC
mà: AC > AB => CD > BD => D thuộc BM (2)
(1) và (2) => D thuộc HM hay D là điểm nằm giữa H và M.
Đúng 0
Bình luận (0)
+Nhận xét: D luôn nằm giữa H và M.
+Chứng minh: AD là đường phân giác của ∆ABC.
=>ABAC=DBDCABAC=DBDC AB < AC
=>DB < DC => DB + DC < DC + DC
=>BD + DC < 2DC hay BC < 2DC => DC >BC2BC2
Mà MC=BC2MC=BC2 (M là trung điểm của BC)
=>DC > MC =>M nằm giữa D và C (1)
+Mặt khác: ˆCAH=900–^CCAH^=900–C^ (∆CAH vuông tại H)
^A+^B+^C=1800A^+B^+C^=1800 (tổng 3 góc ∆ABC)
=>ˆCAH=^A+^B+^C2–^CCAH^=A^+B^+C^2–C^
=>ˆCAH=^A2+^B2–^C2=^A2+^B–^C2CAH^=A^2+B^2–C^2=A^2+B^–C^2
Vì AB < AC =>ˆC<ˆB⇒ˆB–ˆC>0C^<B^⇒B^–C^>0
Do đó: ˆCAH>^A2CAH^>A^2 hay ˆCAH>ˆCADCAH^>CAD^
=>Tia AD nằm giữa hai tia AH và AC =>D nằm giữa hai điểm H và C (2)
Từ (1) và (2) => D nằm giữa H và M.
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH, AB=6cm,BC=10cm vẽ đường phân giác AD của tam giác ABC,đường phân giác DE của tam giác ADB, đường phân giác DF của tam giác ADC.
chứng minh EA/EB.DB/DC.FC/FA=1
cho tam giác ABC, đường phân giác AD, trên nửa mặt phẳng bờ BC ko chứa A vẽ tia Bx sao cho góc BAD =góc CBx. gọi M là giao điểm của AD và Bx
a)c/m tam giác MBD đồng dạng vs tam giác MAB
b)vẽ tia phân giác góc ABC cắt AD ở I .C/M tam giác MBI cân
c)từ M vẽ đường thẳng vng góc vs MA cắt đường cao xuất phát từ A của tam giác ABC tại E ,cắt BC tại F. c/m tam giác EIF vuông
a) Xét tam giác MBD và tam giác MAB:
\(\widehat{DMB}chung.\)
\(\widehat{DBM}=\widehat{BAM}\left(\widehat{CBx}=\widehat{BAD}\right).\)
=> Tam giác MBD \(\sim\) Tam giác MAB (g - g).
Đúng 3
Bình luận (1)