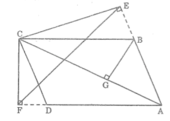
Bài 2 : Cho hình bình hành ABCD, có đường chéo lớn AC. Từ C kẻ CE vuông góc AB, CF vuông góc AD ; BH vuông góc AC. Chứng minh : a) AB.AE = AH.AC b) BC.AF = AC.HC c) AB.AE + AD.AF = AC2 . d) Cho biết CE = 16cm, CF = 20cm, chu vi ABCD = 108cm. Tính diện tích ABCD
Giúp mk vs khó quá



 ⇒ BC.AF = AC.CG
⇒ BC.AF = AC.CG


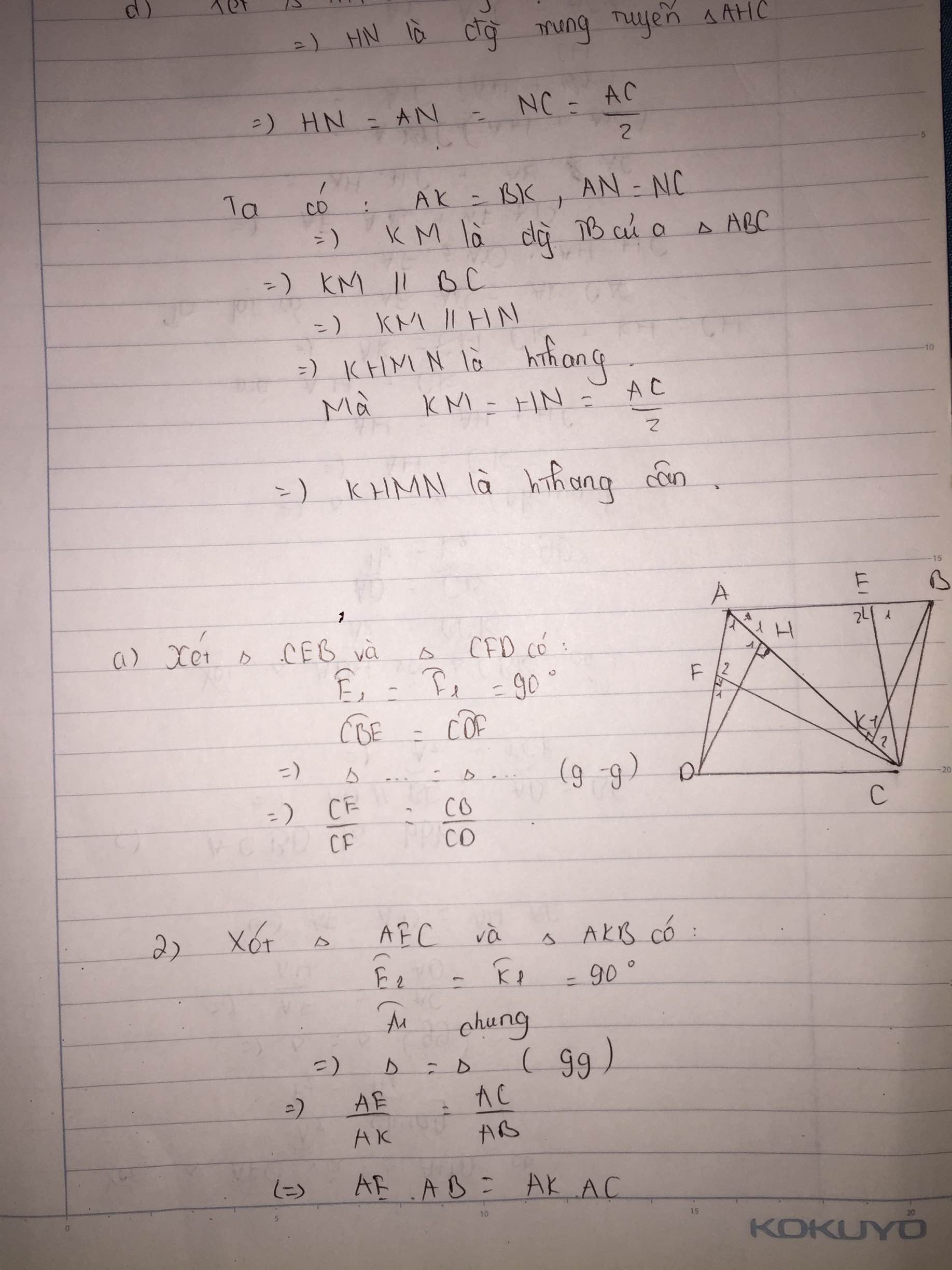
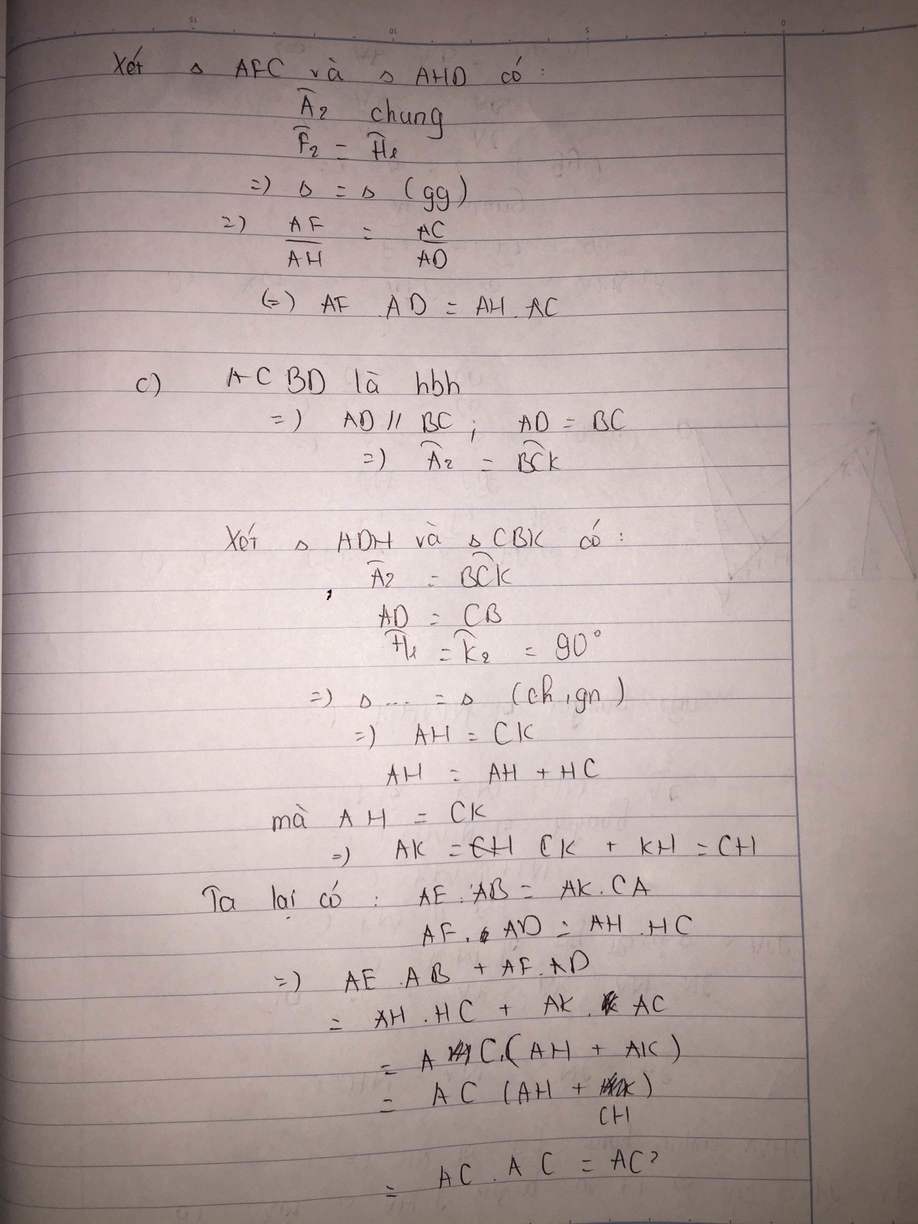

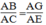
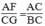 ⇒ BC.AF = AC.CG
⇒ BC.AF = AC.CG