a: Xét ΔADE và ΔBDE có 

DA=DB

DE chung

AE=BE

Do đó: ΔADE=ΔBDE

a: góc ADH=góc AEH=góc DAE=90 độ

=>ADHE là hình chữ nhật

b: ΔAHB vuông tại H có HD là đường cao

nên AD*AB=AH^2

ΔAHC vuông tại H có HE là đường cao

nên AE*AC=AH^2=AD*AB

=>AE/AB=AD/AC

=>ΔAED đồng dạng với ΔABC

c: ΔAED đồng dạng với ΔABC

=>\(\dfrac{S_{AED}}{S_{ABC}}=\left(\dfrac{ED}{BC}\right)^2=\dfrac{4}{25}\)

=>\(S_{AED}=\dfrac{4}{25}\cdot80=\dfrac{320}{25}=12.8\left(cm^2\right)\)

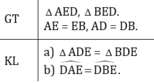
ΔADE và ΔBDE có:

    DE cạnh chung

    AD = BD (gt)

    AE = BE (gt)

Vậy ΔADE = ΔBDE (c.c.c)

(hình tự vẽ,gt kl tự viết).

a) xét \(\Delta ADB\) và \(\Delta EDC\) có:

góc BAD = góc CED(=90 độ)

góc BDA = góc CDE(đối đỉnh)

=> \(\Delta ADB\sim\Delta EDC\left(g.g\right)\)

b) xét \(\Delta ADE\) và \(\Delta BDC\) có:

\(\dfrac{DE}{DB}=\dfrac{AD}{DC}\left(\Delta ADB\sim\Delta EDC\right)\)

góc ADE = góc BDC ( đối đỉnh )

=> \(\Delta ADE\sim\Delta BDC\left(c.g.c\right)\)

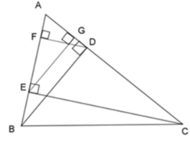
Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)

Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)

=>  => AF.AC = AE.AD (2)

Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF

Đáp án: B

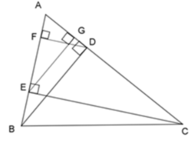
Từ câu trước ta có: A E A B = A G A D = E G B D => AE.AD = AB.AG (1) nên A đúng

Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)

=> A F A E = A D A C => AF.AC = AE.AD (2) nên B đúng

Ngoài ra A D A C = F D E C  => AD.EC = AC.FD nên C đúng

Chỉ có đáp án D sai vì  A E E G = A B B D

Đáp án: D