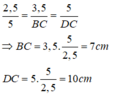Cho hình thang ABCD( AB//CD).Biết AB=2,5cm; AD=3,5cm; BD=5cm.Góc DAB=DBC
a.Chứng minh tam giác ADB đồng dạng với tam giác BCD
b.Tính BC và CD
c. Tính tỉ số diện tích tam giác ADB và BCD
Cho hình thang ABCD (AB//CD) có AB = AD = 1/2 CD. Tính SABCD biết AB = 2,5cm và BD = 4cm
Dựng hình thang cân ABCD(AB // CD) biết BC = 3cm, AB = 2cm, đường cao bằng 2,5cm.
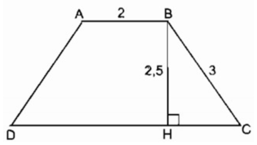
Cách dựng:
- Dựng ∆ BHC, BH = 2,5 cm
- ∠ (BHC) = 90 0
- Trên tia Hx lấy điểm C sao cho BC = 3cm
- Dựng tia đi qua B và song song CH nằm trên nửa mặt phẳng bờ BC chứa điểm H. Lấy điểm A sao cho BA = 2cm
- Dựng cung tròn tâm B bán kính bằng AC cắt tia CH tại D.
Nối AD ta có hình thang ABCD cần dựng.
Chứng minh: Thật vậy theo cách dựng AB // CD nên tứ giác ABCD là hình thang có AB = 2cm, BC = 3cm, BH = 2,5cm.
AC = BD
Vậy ABCD là hình thang cân thỏa mãn điều kiện bài toán.
cho hình thang ABCD biết AB=3cm, CD=6cm, AD=2,5cm. Vẽ đường cao AH,BK. Tính DH,DK,AH
mog các bạn có tâm giúp tôi lm nhanh câu hỏi này
xin chân thành cảm ơn rất nhiều =)))
dung la de bai co van de ABCD phai la hinh thang cân moi du yeu to de lam bai,bn xem lai
dựng hình thang ABCD, biết AD//BC, AB=6cm, aB=3cm, CD=2,5cm và góc A=35. với các dữ kiên trên ta dựng dược mấy hình thang
Cho hình thang ABCD ( A B / / C D ) c ó A B = A D = C D / 2 . Gọi M là trung điểm của CD và H là giao điểm của AM và BD.
a) Chứng minh tứ giác ABMD là hình thoi
b) Chứng minh BD ⊥ BC
c) Chứng minh ΔAHD và ΔCBD đồng dạng
d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.

a) Ta có: AB = AD = CD/2 và M là trung điểm của CD (gt)
⇔ AB = DM và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của ΔBDC mà MB = MD = MC. Do đó ΔBDC là tam giác vuông tại B hay DB ⊥ BC
c) ABMD là hình thoi (cmt) ⇔ ∠D1 = ∠D2
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
![]()
Xét tam giác vuông AHB, ta có :

Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
⇒ BC = AM = 3 (cm)
Ta có:
![]()
M là trung điểm của DC nên
SBMD = SBMC = SBCD/2 = 3 (cm2) (chung đường cao kẻ từ B và MD = MC)
Mặt khác ΔABD = ΔMDB (ABCD là hình thoi)
⇔ SABD = SBMD = 3 (cm2)
Vậy SABCD = SABD + SBMD + SBMC = 9 (cm2)
: Cho hình thang ABCD( AB //CD).
Biết AB = 3cm; AD = 2,5cm;BD = 6cm và DBC = DAB .
a. Chứng minh hai tam giác ADB và BCD đồng dạng.
b. Tính độ dài các cạnh BC và CD
a: Xét ΔADB và ΔBCD có
\(\widehat{BAD}=\widehat{DBC}\)
\(\widehat{ABD}=\widehat{BDC}\)
Do đó: ΔADB\(\sim\)ΔBCD
b: ta có:ΔADB\(\sim\)ΔBCD
nên AD/BC=AB/BD
=>2,5/BC=1/2
hay BC=5(cm)
Cho hình thang ABCD (AB //CD). Biết AB = 2,5cm; AD = 3,5cm; BD = 5cm; và góc DAB = DBC.
a) Chứng minh hai tam giác ADB và BCD đồng dạng.
b) Tính độ dài các cạnh BC và CD
a: Xét ΔADB và ΔBCD có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔADB đồng dạng với ΔBCD
b: ΔADB đồng dạng với ΔBCD
=>AD/BC=DB/CD=AB/BD
=>3,5/BC=5/CD=2,5/5=1/2
=>BC=7cm; CD=10cm
Cho hình thang ABCD (AB // CD) có AB = AD = CD/2. Gọi M là trung điểm của CD và H là giao điểm của AM và BD. a) Chứng minh tứ giác ABMD là hình thoi b) Chứng minh BD ⊥ BC c) Chứng minh ΔAHD và ΔCBD đồng dạng d) Biết AB = 2,5cm; BD = 4cm. Tính độ dài cạnh BC và diện tích hình thang ABCD.
a ) Ta có : \(AB=AD=\frac{CD}{2}\) và M là trung điểm của CD (gt)
\(\Leftrightarrow AB=DM\) và AB // DM
Do đó tứ giác ABMD là hình bình hành có AB = AD. Vậy ABMD là hình thoi.
b) M là trung điểm của CD nên BM là trung tuyến của \(\Delta BDC\) mà MB = MD = MC.
Do đó \(\Delta BDC\) là tam giác vuông tại B hay \(DB\perp BC\)
c) ABMD là hình thoi (cmt) \(\Leftrightarrow\widehat{D}_1=\widehat{D}_2\)
Do đó hai tam giác vuông AHD và CBD đồng dạng (g.g)
d) Ta có :
\(HB=HD=\frac{1}{2}BD=\frac{1}{2}.4=2\left(cm\right)\)
Xét tam giác vuông AHB, ta có :
\(AH=\sqrt{AB^2-HB^2}\) ( định lí Pitago )
\(=\sqrt{2,5^2-2^2}=1,5\left(cm\right)\)
\(\Rightarrow AM=3\left(cm\right)\)
Dễ thấy tứ giác ABCM là hình bình hành (AB // CM và AB = CM)
\(\Rightarrow BC=AM=3\left(cm\right)\)
Ta có :
\(S_{BDC}=\frac{1}{2}BD.BC=\frac{1}{2}.4.3=6\left(cm^2\right)\)
M là trung điểm của DC nên
\(S_{BMD}=S_{BMC}=\frac{S_{BCD}}{2}=3\left(cm^2\right)\)
(chung đường cao kẻ từ B và MD = MC)
Mặt khác \(\Delta ABD=\Delta MDB\) ( ABCD là hình thoi )
\(\Leftrightarrow S_{ABD}=S_{BMD}=3\left(cm^2\right)\)
Vậy \(S_{ABCD}=S_{ABD}+S_{BMD}+S_{BMC}=9\left(cm^2\right)\)
Chúc bạn học tốt !!!
Cho hình thang ABCD có AB//CD ,DA và CB cắt nhau ở M.Biết MA:MD=3:5 và DC=2,5cm .Tính AB
- Đề bài đúng nhé bạn:
Xét tam giác MDC có:
AB//CD (gt)
=>\(\dfrac{MA}{MD}\)=\(\dfrac{AB}{DC}\)(định lí Ta-let)
=>\(\dfrac{AB}{2,5}=\dfrac{3}{5}\)
=>AB=\(\dfrac{3}{5}.2,5\)=1,5(cm)
Hình thang ABCD (AB // CD) có AB =2,5cm, AD = 3,5cm, BD=5cm và ∠ (DAB) = ∠ (DBC). Tính độ dài BC, CD.
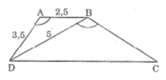
Vì
△
ABD ∼
△
BDC nên: 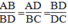
Với AB = 2,5cm; AD = 3,5cm; BD = 5cm, ta có: