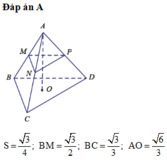
Cho tứ diện đều ABCD có cạnh a. Lấy các điểm B',C' trên AB và AC sao cho AB'=a/2; AC' =2a/3. Tính thể tích khối tứ diện AB'C'D
TT
Những câu hỏi liên quan
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB 2 AM, AN 2NC, AD 2 AP. Thể tích của khối tứ diện AMNP là: A.
a
3
2
72
B.
a
3
3
48
C. ...
Đọc tiếp
Cho tứ diện đều ABCD có cạnh bằng a, trên các cạnh AB, AC, AD lần lượt lấy các điểm M, N, P sao cho AB = 2 AM, AN= 2NC, AD = 2 AP. Thể tích của khối tứ diện AMNP là:
A. a 3 2 72
B. a 3 3 48
C. a 3 2 48
D. a 3 2 12
Cho tứ giác ABCD có diện tích 60cm2. Trên cạnh AB lấy các điểm E, F sao cho AE = EF = FB. Trên cạnh CD lấy các điểm G, H sao cho CG = GH = HD.
a) Tính tổng diện tích các tam giác ADH và CBF.
b) Tính diện tích tứ giác EFGH
Trong không gian với hệ trục tọa độ Oxyz ,cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B,C, D sao cho
A
B
A
B
+
A
C
A
C...
Đọc tiếp
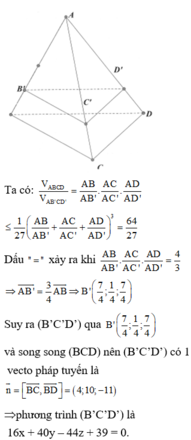
Trong không gian với hệ trục tọa độ Oxyz ,cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, AD lần lượt lấy các điểm B',C', D' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB'C'D' có thể tích nhỏ nhất. Phương trình mặt phẳng (B'C'D') là
A. 16x-40y-44z+39=0
B. 16x-40y-44z-39=0
C. 16x+40y+44z-39=0
D. 16x+40y-44z+39=0
Chọn D
Trên cạnh AB, AC , AD của tứ diện ABCD lần lượt có các điểm B', C', D'. Áp dụng công thức tỷ số thể tích ta có
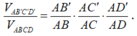
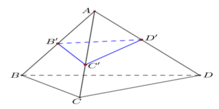
Từ giả thiết
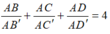
áp dụng bất đẳng thức AM- GM ta có
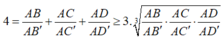
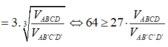
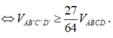
Do thể tích ABCD cố định nên thể tích AB'C'D' nhỏ nhất
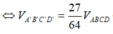
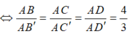
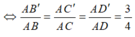
=> (B'C'D') song song với (BCD) và đi qua điểm B'
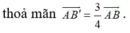
![]()
![]()
suy ra vectơ pháp tuyến của mặt phẳng (B'C'D') là:
![]()
![]()
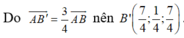
Vậy phương trình (B'C'D') là:
![]()
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho
A
B
A
B
+
A
C
A
C
+
A
D...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A(1;1;1), B(2;0;2), C(-1;-1;0), D(0;3;4). Trên các cạnh AB, AC, ADlần lượt lấy các điểm B’,C’,D’ sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện AB’C’D’ có thể tích nhỏ nhất. Phương trình mặt phẳng (B’C’D’) là
A. 16x-40y-44z-39=0.
B. 16x-40y-44z+39=0.
C. 16x+40y+44z-39=0.
D. 16x+40y-44z+39=0.
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B, C, D sao cho thể tích của khối tứ diện ABCD nhỏ nhất và
A
B
A
B
+
A
C
A
C
+
A...
Đọc tiếp
Trong không gian Oxyz, cho tứ diện ABCD có A (1;1;1), B (2;0;2), C ( -1;-1;0) và D ( 0;3;4). Trên các cạnh AB , AC, AD lần lượt lấy các điểm B', C', D' sao cho thể tích của khối tứ diện AB'C'D' nhỏ nhất và A B A B ' + A C A C ' + A D A D ' = 4 . Tìm phương trình của mặt phẳng (B’C’D’)
A. 16 x + 40 y - 44 z + 39 = 0
B. 16 x - 40 y - 44 z + 39 = 0
C. 16 x + 40 y + 44 z + 39 = 0
D. 16 x + 40 y - 44 z - 39 = 0
Cho hình bình hành ABCD . Trên các cạnh AB và CD lấy các điểm E và F sao cho AE=CF, trên các cạnh AD và BC lấy điểm M và N sao cho AM=CN a) Tứ giác MENF là hình gì ? Vì sao ? b) Chứng minh các đường thẳng AC,BD,EF và MN đồng quy . c) Nếu AE = CF = AB : 2 và AM = CN = AD : 2 thì tứ giác MENF là hình gì Giúp mk với!!!!!!!!
Xem chi tiết
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm
A
1
;
1
;
1
,
B
2
;
0
;
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho tứ diện ABCD có tọa độ các điểm A 1 ; 1 ; 1 , B 2 ; 0 ; 2 , C - 1 ; - 1 ; 0 , D 0 ; 3 ; 4 . Trên các cạnh AB, AC, AD lần lượt lấy các điểm B ' , C ' , D ' sao cho A B A B ' + A C A C ' + A D A D ' = 4 và tứ diện A B ' C ' D ' có thể tích nhỏ nhất. Phương trình măt phẳng B ' C ' D ' là
A. 16 x - 40 y - 44 z + 39 = 0
B. 16 x + 40 y + 44 z - 39 = 0
C. 16 x + 40 y - 44 z + 39 = 0
D. 16 x - 40 y - 44 z - 39 = 0
Chọn đáp án C
Áp dụng công thức tỉ số thể tích ta có:
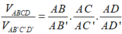
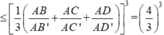
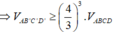
Suy ra thể tích tứ diện AB'C'D' nhỏ nhất khi
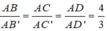
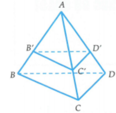
Khi đó A B ' ⇀ = 3 4 A B ⇀ và B ' C ' D ' / / B C D
⇒ Mặt phẳng B ' C ' D ' có một vec-tơ pháp tuyến là
![]()
Lại có
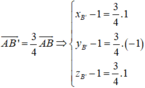
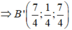
Phương trình mặt phẳng B ' C ' D '
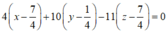
![]()
Đúng 0
Bình luận (0)
cho hình vuông abcd có cạnh bằng 4cm trên các cạnh ab,bc,cd,da lần lượt lấy các điểm e,f,g,h sao cho ae=bf=cg=dh=1cm A) tứ giác efgh là hình gì? B) tính diện tích của efgh? C) Xác định vị trí của e,f,g,h trên cạnh (ab=bc=cd=da) sao cho diện tích tứ giác efgh nhỏ nhất
a: AE+EB=AB
BF+FC=BC
CG+GD=CD
DH+HA=DA
mà AB=BC=CD=DA và AE=BF=CG=DH
nên EB=FC=GD=HA
Xét ΔEAH vuông tại A và ΔGCF vuông tại C có
EA=GC
AH=CF
Do đó: ΔEAH=ΔGCF
=>EH=GF
Xét ΔEBF vuông tại B và ΔGDH vuông tại D có
EB=GD
BF=DH
Do đó: ΔEBF=ΔGDH
=>EF=GH
Xét ΔEAH vuông tại A và ΔFBE vuông tại B có
EA=FB
AH=BE
Do đó: ΔEAH=ΔFBE
=>EH=EF và \(\widehat{AEH}=\widehat{BFE}\)
\(\widehat{AEH}+\widehat{HEF}+\widehat{BEF}=180^0\)
=>\(\widehat{BFE}+\widehat{BEF}+\widehat{HEF}=180^0\)
=>\(\widehat{HEF}+90^0=180^0\)
=>\(\widehat{HEF}=90^0\)
Xét tứ giác EHGF có
EF=GH
EH=GF
Do đó: EHGF là hình bình hành
Hình bình hành EHGF có EF=EH
nên EHGF là hình thoi
Hình thoi EHGF có \(\widehat{HEF}=90^0\)
nên EHGF là hình vuông
b:
AH+HD=AD
=>AH+1=4
=>AH=3(cm)
ΔAEH vuông tại A
=>\(AE^2+AH^2=EH^2\)
=>\(EH^2=3^2+1^2=10\)
=>\(EH=\sqrt{10}\left(cm\right)\)
EHGF là hình vuông
=>\(S_{EHGF}=EH^2=10\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Hãy tính góc giữa các cặp vecto sau đây:a)
A
B
→
v
à
B
C
→
b)
C
H
→
v
à
A
C
→
Đọc tiếp
Cho tứ diện đều ABCD có H là trung điểm của cạnh AB. Hãy tính góc giữa các cặp vecto sau đây:
a) A B → v à B C →
b) C H → v à A C →
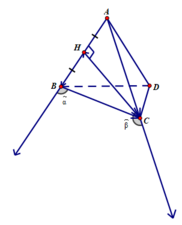
Tứ diện ABCD đều có các mặt là tam giác đều
a) Góc giữa A B → v à B C → là góc α ^ và
α ^ = 180 o - 60 o = 120 o
b) Góc giữa C H → v à A C → là β ^
H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB
Xét tam giác vuông ACH tại H có
A C H ^ + H A C ^ = 90 o ⇒ A C H ^ = 90 o - 60 o = 30 o
Nên β ^ = 180 o - 30 o = 150 o
Đúng 0
Bình luận (0)