Co tam giác ABC có góc A=600. Các tia phân giác của các góc B và C cắt nhau tại I và cắt AC; AB theo thứ tự tại D,E. Chứng minh rằng ID=IE.( Vẽ hình nữa nhé!)
HG
Những câu hỏi liên quan
Tam giác ABC có
A
^
60
°
các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc
B
I
C
^
;
B
K
C
^
. A.
B...
Đọc tiếp
Tam giác ABC có A ^ = 60 ° các tia phân giác của góc B và C cắt nhau tại I. Các tia phân giác góc ngoài tại đỉnh B và C cắt nhau tại K. Tính các góc B I C ^ ; B K C ^ .
A. B I C ^ = 100 ° ; B K C ^ = 80 °
B. B I C ^ = 90 ° ; B K C ^ = 90 °
C. B I C ^ = 60 ° ; B K C ^ = 120 °
D. B I C ^ = 120 ° ; B K C ^ = 60 °
Đáp án cần chọn là: D
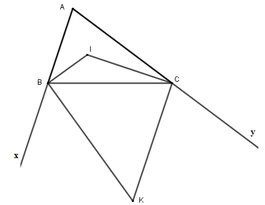
Xét tam giác ABC có:

Đúng 0
Bình luận (0)
Cho tam giác ABC. Các tia phân giác của góc B và góc C cắt nhau tại I. Các tia phân giác của các góc ngoài đỉnh B và C cắt nhau tại K. Tính số đo góc BIC và góc BKC theo số đo góc A của tam giác ABC
Bạn xem ở đường link này:
Câu hỏi của Cùng học toán đi - Toán lớp 6 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC. Các tia phân giác của góc B và góc C cắt nhau tại I. Các tia phân giác của các góc ngoài đỉnh B và C cắt nhau tại K. Tính số đo góc BIC và góc BKC theo số đo góc A của tam giác ABC
Hình vẽ a chèn không rõ được không, chắc giống của e thôi.
https://1drv.ms/u/s!AhUPZHs4UJtKilHrVZWqF8i6a584?e=0TIfMP
Ta có : \(\widehat{BIC}=180^0-\widehat{IBC}-\widehat{ICB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BIC}=180^0-\frac{\widehat{ABC}}{2}-\frac{\widehat{ACB}}{2}\)( Do IB,IC là tia phân giác của góc ABC và ACB)
còn \(\widehat{BKC}=180^0-\widehat{KBC}-\widehat{KCB}\)( Do tổng ba góc trong một tam giác bằng 180 độ)
\(\Rightarrow\widehat{BKC}=180^0-\frac{\widehat{xBC}}{2}-\frac{\widehat{yCB}}{2}\)( Do KB,KC là tia phân giác của góc ABC và ACB)
Mà \(\hept{\begin{cases}\widehat{xBC}=180^0-\widehat{ABC}\\\widehat{yCB}=180^0-\widehat{ACB}\end{cases}}\)\(\Rightarrow\widehat{BKC}=180^0-\left(\frac{180^0-\widehat{ABC}}{2}+\frac{180^0-\widehat{ACB}}{2}\right)\)
\(\Rightarrow\widehat{BKC}=\frac{\widehat{ABC}}{2}+\frac{\widehat{ACB}}{2}\)
Cho tam giác ABC có góc A = 60 độ. Các tia phân giác của góc B và góc C cắt nhau ở I. các tia phân giác ngoài của góc B và góc C cắt nhau ở K. Tia phân giác góc B cắt tia phân giác góc ngoài ở đỉnh C tại E. Tính góc BIC, BKC, BEC.
cho tam giác ABC vuông tại A có AB < AC.
a, So sánh các góc của tam giác ABC.
b, tia phân giác của góc ABC và tia phân giác của góc ACB cắt nhau tại I. So sánh IB và IC.
c, gọi d là đường thẳng vuông góc với BC tại C. tia BI kéo dài cắt AC ở D và cắt đường thẳng d tại M. chứng minh CDM = CMD
a:
ΔABC vuông tại A nên BC là cạnh lớn nhất
=>AC<BC
mà AB<AC
nên AB<AC<BC
Xét ΔABC có AB<AC<BC
mà \(\widehat{C};\widehat{B};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Ta có: \(\widehat{ABI}=\widehat{CBI}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACI}=\widehat{BCI}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ACB}< \widehat{ACB}\)
nên \(\widehat{ICB}< \widehat{IBC}\)
Xét ΔIBC có \(\widehat{ICB}< \widehat{IBC}\)
mà IB,IC lần lượt là cạnh đối diện của các góc ICB và góc IBC
nên IB<IC
Đúng 1
Bình luận (1)
Cho tam giác ABC có góc A bằng 60 độ. Các tia phân giác của góc B và góc C cắt nhau ở I. Các tia phân giác ngoài của góc B và góc C cắt nhau ở K. Tia phân giác góc B cắt tia phân giác ngoài ở đỉnh C tại E. Tính góc BIC, BKC, BEC
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
Đúng 0
Bình luận (0)
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
⇒ góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
⇒ góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
Ai trên 10 điểm hỏi đáp thì mình nha mình đang cần gấp chỉ còn 99 điểm là tròn rồi mong các bạn hỗ trợ mình sẽ đền bù xứng đáng
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A = 60 độ. Các tia phân giác của góc B và góc C cắt nhau tại I, cắt AB và AC ở D và E. Tia phân giác góc BIC cắt BC ở F
a) Tính góc BIC
b) Chứng minh: ID = IE = IF
c) Chứng minh: Tam giác EDF đều
a: Xét ΔABC có
\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)
\(\Leftrightarrow2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-60^0=120^0\)
\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=60^0\)
\(\Leftrightarrow\widehat{BIC}=120^0\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A= 60 độ. Các tia phân giác của góc B và góc C cắt nhau ở I. Các tia phân giác ngoài của goác B và C cắt nhau ở K. Tia phân giác góc B cắt tia phân giác góc ngoài ở đỉnh C tại E. Tính góc BIC, BKC, BEC.
Hsshjdcj j u5ufn n u ìbg
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.Bài 2: Cho tam giác ABC có góc A 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM...
Đọc tiếp
Bài 1: Cho tam giác ABC, hai đường phân giác BD và CE của tam giác cắt nhau tại O. Tia AO cắt BC tại M. Tam giác ABC phải có điều kiện gì để AM vuông góc với BC.
Bài 2: Cho tam giác ABC có góc A= 50°. Đường phân giác của góc B và đường phân giác ngoài tại đỉnh C của tam giác cắt nhau tại O. Tính số đo góc BAO.
Bài 3: Cho tam giác ABC, các tia phân giác của các góc B và C cắt nhau tại O. Từ A vẽ một đường thẳng vuông góc với OA, cắt các tia BO và CO lần lượt tại M và N. CMR: BM vuông góc với BN, CM vuông góc với CN.
Mọi người giúp mình nhanh nha😙😙😙😙
Câu hỏi của Nguyễn Quang Nam - Toán lớp 8 - Học toán với OnlineMath
Tham khảo bài 3 tại link trên nhé!
Đúng 0
Bình luận (0)



