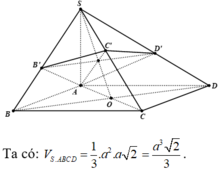
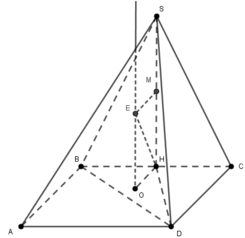
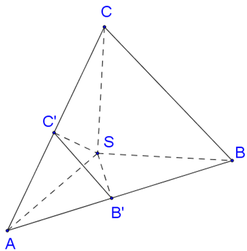
Cho hình chóp S . A B C có S A = a ; A B = a 3 ; B A C ^ = 150 o và S A vuông góc với mặt phẳng đáy. Gọi M , N lần lượt là hình chiếu vuông góc của A trên SB và SC. Thể tích khối cầu ngoại tiếp hình chóp A . B C M N bằng.
A. 4 7 π a 3 3
B. 44 11 π a 3 3
C. 28 7 π a 3 3
D. 20 5 π a 3 3