Bài 4: (3 điểm) Cho đường tròn (O; R), đường kính MN. Qua M và N vẽ lần lượt hai tiếp tuyến (d) và (d’) với đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở A và cắt đường thẳng (d’) ở P. Từ O vẽ một tia vuông góc với AP và cắt đường thẳng (d’) ở B.
Chứng minh OA = OP . OH vuông góc với AB. Chứng minh OH = R và AB là tiếp tuyến của đường tròn (O).
Chứng minh AM.BN = R2.
Tìm vị trí của điểm A để diện tích tứ giác ABNM nhỏ nhất. Vẽ hình minh họa trong trường hợp này.

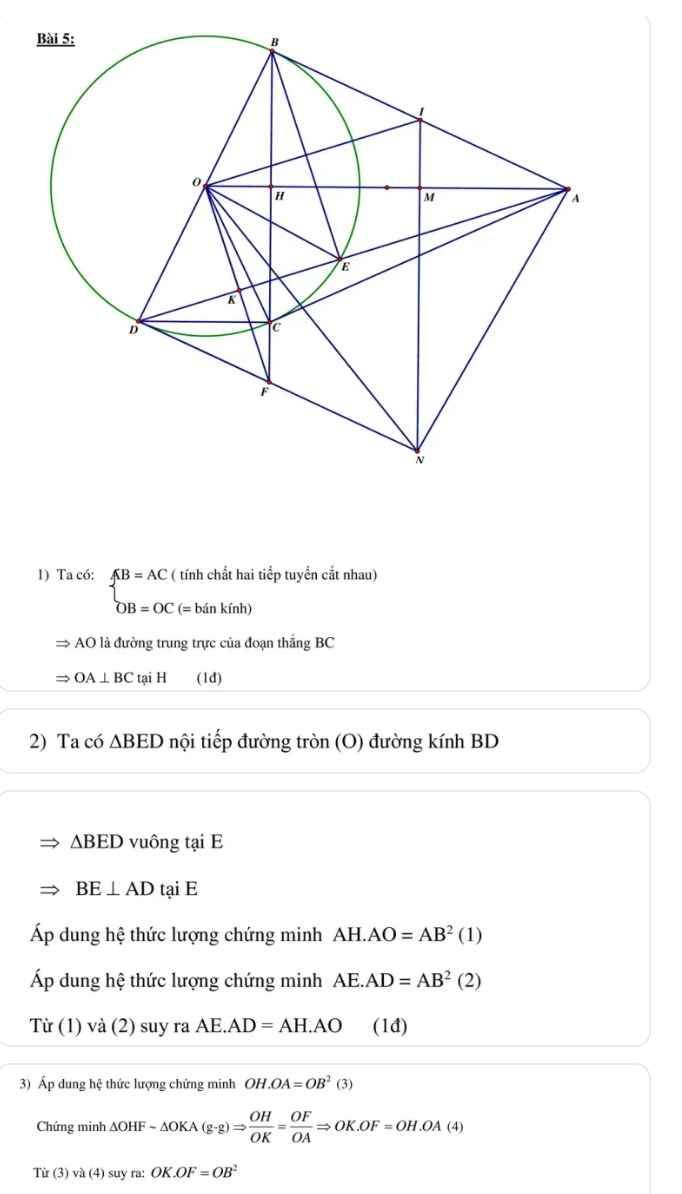
Bài 6: Cho đường tròn (O) và một điểm A nằm ngoài đường tròn (O). Từ A vẽ hai tiếp tuyến AB, AC của đường tròn (O) (B và C là hai tiếp điểm). Gọi H là giao điểm của OA và BC

a) Chứng minh OA vuông góc với BC tại H
b) Từ B vẽ đường kính BD của (O), đường thẳng AD cắt đường tròn (O) tại E (khác D), Chứng minh: AE.AD=AH.AO
c) Qua O vẽ đường thẳng vuông góc với cạnh AD tại K và cắt đường BC tại F. Chứng minh FD là tiếp tuyến của đường tròn tâm (O)

d) Gọi I là trung điểm cạnh AB, qua I vẽ đừng thẳng vuông góc với cạnh AO tại M và đường thẳng này cắt đường thẳng DF tại N. Chứng minh: ND=NA

Bài 5  Cho nửa đường tròn (O) đường kính AB. Trên tia dối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB

a, c/m tia CA là tia phân giác của góc MCH

b, Giả sử MA = a, MC = 2a. Tính AB và CH theo a

Bài 6  Cho tam giác ABC ngoại tiếp đường tròn (O). Gọi D,E,F lần lượt là các tiếp điểm của đường tròn trên các cạnh AB,BC,CA. Gọi M,N,P lần lượt là các giao điểm của đường tròn (O) với các tia OA,OB,OC. c/m các điểm M,N,P lần lượt là tâm của đường tròn nội tiếp các tam giác ADF, BDE và CEF

Bài 1 : Cho đường tròn tâm O đường kính AB . Trên cùng nửa mặt phẳng bờ AB , kẻ hai tiếp tuyến Ax và By với đường tròn ( O ) , trên tia By lấy điểm D sao cho góc COD = 90⁰ , tia CO cắt tia đối của tia By ở E .

a, Chứng minh tam giác CDE là tam giác cân .

b, Chứng minh CD là tiếp tuyến của đường tròn ( O) .

Bài 2 : Cho tam giác ABC vuông tại A , đường cao AH . Đường tròn tâm ( I) đường kính BH cắt AB tại D , đường tròn tâm (K ) đường kính CH cắt AC tại E .

a, Tứ giác ADHE là hình gì ? Vì sao ?

b, Chứng mình rằng DE là tiếp tuyến chung của ( I ) và ( K )

Các bạn ơi ! giúp mình với đi !!

Bài 1: Cho đường tròn (O;R),đượng kính AB,qua A và B vẽ lần lượt hai tiếp tuyến d và d' với đường tròn (O) , một đường thẳng qua O cắt d ở M, cắt d' ở P.Từ O vẽ một đường vuông góc với MP và cắt d' tại N

a) Cm ON=OP và △NMP cân

b)Cm AN.BN=R2

c) Cm AB là tiếp tuyến của đường tròn,đường kính MN

d)M di chuyển trên đường thẳng d,tìm vị trí của M để Stứ giác AMNB là nhỏ nhất

bài 1: tam giác ABC nhọn nội tiếp đường tròn tâm O có 3 đường cao AK,BD,CE cắt nhau tại H.

a) CM : BEDC nội tiếp

b) CM : H là tâm đường tròn nội tiếp tam giác DEK

Bài 2 : tam giác ABC nhọn nội tiếp đường tròn tâm O, 2 đường cao BM và CN của tam giác cắt nhau tại H.

a) BCMN nội tiếp

b) AM.AC = AN.AB

c) tia AO cắt đường tròn tâm O tại K cắt MN tại I. CM : H,K,E thẳng hàng ( E là trung điểm BC)

Bài 3  Cho tam giác ABC (AB<AC) nội tiếp trong đường tròn (O). Vẽ đường kính MN vuông góc BC (điểm M thuộc cung BC ko chứa A). c/m các tia AM, AN lần lượt là các tia phân giác trong và ngoài tại đỉnh A của tam giác ABC

Bài 4  Cho đường tròn (O) và 2 dây MA, MB vuông góc với nhau. Gọi I,K lần lượt là điểm chính giữa của các cung nhỏ MA và MB. Gọi P là giao điểm của AK và BI

a, c/m 3 điểm A,O,B thẳng hàng

b, c/m P là tâm đường tròn nội tiếp tam giác MAB

c, giả sử MA =12cm, MB = 16cm, tính bán kính của đường tròn nộ tiếp tam giác MAB 

Bài 9 : Cho tam giác ABC có 3 góc nhọn ( AB<AC) . Vẽ 2 đường cao BE và CF của tam giác ABC cắt nhau tại H .Đường tròn tạm O , đường kính CH cắt BC tại K . Các tiếp tuyến tại E và C của (O) cắt nhau tại M . Chứng minh :

1/Tứ giác OEMC , BFEC nội tiếp được

2/HF.HC=HB.HE

3/3 điểm A,H,K thẳng hàng và I,O,M thẳng hàng

4/ 5 điểm E,F,K,I,O cùng thuộc 1 đường tròn

5/Kẻ tiếp tuyến BT đến O ( T là tiếp điểm , T thuộc cung nhỏ KC ) ,FT cắt (O) tại G , EG cắt AB tại S .Chứng minh : tứ giác SBKT nội tiếp

6/ Chứng tỏ : 3 đường thẳng BM,FC,AT đồng quy tại 1 điểm

Ai giỏi toán giúp em bài này với vẽ hình giúp em

Cho \(\Delta ABC\)nhọn. Đường tròn ( O ) đường kính BC cắt AB, AC lần lượt tại E và D. Các tiếp tuyến của ( O ) tại D và E cắt nhau tại M.

Gọi H là giao điểm của BD và CE. CMR:

a, 4 điểm A, E, H, D cùng thuộc 1 đường tròn. Gọi đường tròn đó là ( I )

b, IE là tiếp tuyến của ( O )

c, AM \(\perp\)BC 

Câu 1:Cho 2 góc kề nhau aOb,aOc sao cho aOb = 35 độ và aOc = 55 độ. Gọi Om là tia đối của tia Oc.

a)Tính số đo góc aOm và bOm

b)Gọi On là tia phân giác của góc bOm. Tính số đo góc aOn

c)Vẽ tia đối của tia On là tia On'. Tính số đo góc mOn.

Câu 2:Cho 2 đường tròn (O;4cm) và (O ; 2cm) sao cho khoảng cách giữa 2 tâm O và O' là 5cm. Đường tròn (O;4cm) cắt đoạn OO' tại điểm A và đường tròn (O;2cm) cắt đoạn OO' tại B.

a)Tính O'A,BO,AB

b)Chứng minh A là trung điểm của đoạn O'B

Bài 1 các bạn ko cần vẽ hình đâu ạ chỉ cần vẽ bài 2 thôi ạ